излучения ). Плотность потока падающего излучения д',-, складывается из частей потоков эффективного излучения всех поверхностей замкнутой системы, достигающих k-ii поверхности. Если к-я новерхность может видеть сама себя (является вогнутой), то часть потока эффективного излучения этой поверхности войдет в выражение для потока падающего излучения. Поток падающего излучения тогда будет равен

A-hqi. k = AiQo, -f A2qo,-iF2-k +

+ Ajqo. jFj-h -f . . . -f Akqo,kFk-k +

+ Л^до.Л ь. (8.3)

Из соотношения взаимности для угловых коэффициентов (7.25) имеем

AiF-k = ЛьП^1, (8.4)

Тогда соотношение (8.3) можно записать в виде Auqt, k = Af,Ff, iqoi 4- AFf,-2qo,2 + . . .

+ A Ff,-jqo,j + . . . + AfFf, f,q +

+ Л ftF h-Nqo,N

или

qi.-k == S Fk-jqo, j-

(8.5a)

(8.56)

Соотношения (8.2) и (8.5) дают два различных выражения для д и- Подставляя их в уравнение (8.1), чтобы исключить д; получают два основных уравнения теплового баланса для потока результирующего излучения Q, выраженного через плотность потока эффективного из.лучения go.ft

Q = Ak{on-qo,k),

(8.6) f(8.7)

Qk = Л (go, k- S Fk-jqo, j) ,

где Qh может рассматриваться как поток излучения, подводимый к поверхности к извне, или как поток результирующего излучения поверхности к внутри замкнутой системы.

) Согласно терминологии по теории теплообмена [15*], термин яркость излучения используется как аналог термину интенсивность излучения. Для обозначения применяется термин плотность потока эффективного излу нения, который и использовали при переводе настоящей книги.- Прим. ред.

Заметим, что уравнения (8.6) и (8.7) можно записать для каждой из TV поверхностей в замкнутой системе. Это дает 2N уравнений с 2N неизвестными. N неизвестных составляют до-Остальные неизвестные будут состоять из Q \i Т ъ зависимости от заданных граничных условий. Как будет показано позже, величины Qa можно исключить. И, такнм образом, останутся урав-нений с TV неизвестными Q ж Т.

Теперь на некоторых примерах покажем, как использовать систему уравнений (8.6) и (8.7).

ПРИМЕР 8.1. Вывести уравнение теплообмена между двумя параллельными бесконечными плоскими пластинами в функции их температур и при > Т^, (фиг. 8.3).

Фиг. 8.3. Тепловые потоки при теплообмене излучением между бесконечными параллельными пластинами.

Так как все излучение, испускаемое одной пластиной, попадает на другую пластину, то F-a = F-i = 1- Запишем уравнения (8.6) и (8.7) для каждой пластины:

= q.-TioTt-qo..h

-J- = gi==go;i-go,2,

ч

= q2-

----- A2{an-qo,2),

I-G2

= ?2 = ?o. 2 -go, 1-

(8.8a) (8.86) (8.9a) (8.96)

Из сравнения (8.86) и (8.96) следует, что = -q, т. е. тепло, подводимое к поверхности 1, отбирается от поверхности 2. П.710т-ность теплового потока определяет таким образом результирующий теплообмен между поверхностями 1 и 2. Уравнение (8.8а) решается относительно go,i

qo,ioTt-~qi.

Подобным образом из уравнения (8.9а) находим

qo,2 = oT\.

92 =

Эти выражения подставляются в (8.86) и оно решается относительно qi

4-1/62 (7-2)-1

(8.10а)

Функциональная зависимость g (Т) введена для того, чтобы показать, что 1 и 2 могут зависеть от температуры. Так как Ti и Т^ заданы, то б^ и можно вычислить при соответствуюш;их температурах, и gi определяется неносредственно.

ПРИМЕР 8.2. Какую температуру примет поверхность 1 при заданной плотности теплового потока и известном значении для системы параллельных пластин из предыдуш;его примера?

Найдем решение уравнения (8.10а) относительно

iiiTi) 62(2)

(8.106)

Так как степень черноты (Т^) яв.11яется функцией Ti, которая неизвестна, то необходимо воспользоваться методом итераций. Выбирается пробное значение Ti и вычисляется при этом значении Tl- Далее решается уравнение (8.106) относительно Ti и полученное значение используется для выбора 61 в следуюш;ем приближении. Процесс продолжается до тех пор, пока 61 (Tl) и Tl не перестанут изменяться в носледуюш;их итерациях.

Сфера г

ПРИМЕР 8.3. Вывести уравнение теплообмена излучением между двумя изотермическими концентрическими диффузно-серыми сферами (фиг. 8.4).

Эта система сложнее системы параллельных пластин, так как поверхности имеют неравные площади и поверхность 2 может частично видеть саму себя. Выражения для угловых коэффициентов для этого случая были выведены в примере 7.13: Fi 2 = 1, F2-\ -1/2, F2-2 = 1 - AIA. Запишем основные уравнения теплового балан-

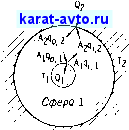
Фиг. 8.4. Тепловые потоки при теплообмене излучением между двумя концентрическими сферами.

Q = A{aT\-qo,i),

Qi = Ai {qo,i - qo, 2), €2

ca (8.6) и (8.7) для каждой из двух сферических поверхностей:

ei / 74 ч (8.11а)

(8.116)

Q2 = A2-j{aTl-qo,2), (8.12а)

(?2 = Л [qo, 29о, 1 - (1 ) до, 2] = 1 (-до, 14-до, а)- (8.126)

Из сравнения (8.11) и (8.12) следует, что = -Q как и следовало ожидать из условия теплового баланса системы. Четыре полученных уравнения можно решить относительно четырех неизвестных д^ i, go, 2, Q\ и Q2 и получить выражение для потока результирующего излучения в следующем виде:

i/ei(ri)-t-(i/2)[i/e2 (Га)-!]

(8.13)

Если сферические новерхности не концентрические, все излучение новерхности 1 все же попадает на поверхность 2. Угловой коэффициент Fi 2 и в этом случае равен 1, и с помощью тех же предположений, как и ранее, получим выражение (8.13). Однако когда сфера 1 относительно мала (например, ее диаметр равен половине диаметра сферы 2), а эксцентриситет велик, то геометрия системы настолько отличается от концентрической, что использование (8.13) будет интуитивно казаться неверным. Ошибка при использованпи уравнения (8.13) связана с тем, что его вывод основан на предположении постоянства д, д^, qo в пределах А^ я А 2- Эти условия строго выполняются только для концентрических сфер.

ПРИМЕР 8.4. Серое изотермическое тело, имеющее поверхность Ах и температуру Ti, полностью охвачено гораздо большей по размерам серой изотермической замкнутой поверхностью площадью А2- Какой поток энергии передается от Л1 к Ла? Поверхность Ai не видит саму себя, т. е. Fx-i = 0.

Так как новерхность Ах полностью охвачена поверхностью и = О, то угловые коэффициенты и сам анализ соответствуют рассмотренному в примере 8.3 случаю, который описывается уравнением (8.13). В настоящем случае Ах <С^2, и это уравнение сводится к следующему:

<?1 = Лб1(?1)а(Г?-Га)-

(8.14)

Заметим, что полученное выражение не зависит от стенени черноты 2 замыкающей новерхности.

ПРИМЕР 8.5. Рассмотрим замкнутую систему, состоящую из трех поверхностей (фиг. 8.5). Замкнутая система имеет достаточную длину, так что при выводе уравнения теи.лового баланса концевыми эффектами можно пренебречь. Какой тепловой поток

Поверхность ь,у

Поверхность 3-

Поверхность 2

Фиг. 8.5. Замкнутая система, состоящая из трех поверхностей (краевые эффекты не учитываются).

надо подвести к каждой поверхности (равный потоку результирующего излучения от каждой поверхности внутри замкнутой системы), чтобы поддерживать эти поверхности при температурах Ti, и Гз? Запишем уравнения (8.6) и (8.7), для каждой из трех поверхностей:

91 J.(art-go,0.

Ai l-€i

= 4o,i - Fi-iQa, 1 - Fi-iQa, 2 - Fi-qo, З) 2 1-2

= Qo, i-Fi-iqo, 1 - р2-2?о, 2 - Fi-qo,3 = ?o, 3 - 3-i?o, 1 - F3 2go, 2 - F3-3Q0, a-

(8.15a) (8.156) (8.16a) (8.166) (8.17a) (8.176)

Первое уравнение каждой из этих трех пар уравнений можно решить относите.льно qo в функции Т ж Q. Эти выражения для до подставляются затем во второе уравнение каждой из трех пар, что дает

2 р -€2 l-2-

Fi-3

Аг €2 Аз ёз

= (1 аТ\- Fi 2<yT\-Fi-3Tl, (8.18а)

Qi р

-F2-iOT\+{i-

62 2-2)

з'- ез

Fo .3on, (8.186)

л. 3-1

l-G 2

2- €2

3 \ ез бз ) ~

Рз 2оТ1 + {\~Гз-з)оП. (8.18в)

Так как температуры Т известны, то значения степеней черноты g могут быть точно определены, и тогда система из этих трех уравнений решается относительно тепловых потоков Q, подводимых к каждой поверхности. Заметим, что полученные решения являются первыми прпб.тижениями, так как поток эффективного излучения каждой поверхности, как и предполагалось, неоднороден. Это связано с тем, что ноток отраженного излучения неоднороден. Бо.лыпая точность может быть получена путем деления каждой из трех поверхностей на несколько участков.

Теперь, когда с помощью нескольких простых примеров получено некоторое представление об уравнениях теплообмена излучением, система уравнений будет рассмотрена в общем виде для замкнутой системы из N поверхностей.

Система уравнений, связывающих поток результирующего излучения Q и температуру поверхности Г. Форма уравнения (8.18) свидетельствует, что потоки результирующего излучения Q и температуры Т для замкнутой системы из TV поверхностей могут быть связаны общей системой из TV уравнений. Уравнение (8.6) решается относительно плотности потока эффективного излучения qo,h-Затем до подставляется в уравнение (8.7). (Заметим что до-находится просто заменой индекса в соотношении для до, ь-) Это приводит к следующему уравнению для fe-й поверхности, которое также очевидно из (8.18):

<?! 27 1 - €l V2 V

--T-fe-i-;---

Q2 If l-€2 ,

\ Qn p 1-€n

=--n iart-F.-2CTr-...+

+ (1 - F, ,) аП - . .. - FyoTh,

Используя знак суммирования, это выражение можно переписать в виде

2 (~-F,,) = (8,f-F,.j)aT% (8.19)