параметров

8690

= 0,60,

РсОг + PnzO 5800 + 8690

/?соЛ + №о. = 2545+ 3820 = 6365 Па-м.

Эта поправка равна = 0,002. Теперь определим степень черноты смеси газов

eg = €со2 + бнго- Аб = 0,039 + 0,031 - 0,002 = 0,068.

Следовательно, ноток излучения газовой области при теоретической температуре горения будет равен \Q = б^ЛаГ| = 0,068.0,93я 5,729 10- .(1853)* = 13,37 10* Вт.

21.4.3. Излучение светящихся пламен

и прохождение через них излучения

Области активного горения пламени присущи некоторые особенности, которые усложняют перенос излучения. Одновременно происходящие выделение и потери энергии вызывают колебания температуры и, следовательно, колебания свойств и излучения пламени. Промежуточные продукты сгорания, образующиеся в сложных химических реакциях, могут существенно отличаться характеристиками излучения от конечных продуктов. Наиболее важным излучающим продуктом сгорания углеводородов является сажа. Она излучает в непрерывном спектре в видимой и инфракрасной областях, и из-за присущего ему видимого излучения пламя называют светящимся. При содержании сажи в продуктах сгорания часто удваивается или утраивается тепловое излучение газообразных продуктов сгорания. Метод увеличения излучения пламени заключается в поддержании слабого начального перемешивания кислорода с горючим, что способствует образованию большого количества сажи в основании пламени.

Задача об определении влияния сажи на излучение пламени решается в два этапа. На первом этапе определяют распределение по размерам частиц сажи в пламени. Оно зависит от типа горючего, перемешивания его с окислителем и температуры пламени. Расчет распределения частиц сажи по размерам, исходя из основных параметров, представляет очень сложную задачу, поэтому приходится использовать экспериментальные результаты для данной системы сжигания топлива. Второй этап заключается в определении радиационных свойств сажи. Лишь только кОгда известны распределение по размерам и концентрация частиц сажи, можно попытаться рассчитать ее излучение. В настоящее время свойства излучения сажи известны только в первом приближении.

Отдельные частицы сажи, образующиеся в углеводородных пламенах в лабораторных условиях и промышленности, имеют диаметры от 5 -10 до 0,3 мкм и более. Саи^а может присутствовать в пламени в виде сферических частиц, агломератов, а иногда в виде-длинных нитей. Экспериментальное определение формы частиц сажи является очень сложной задачей, так как введение в пламя любого зонда с целью отбора частиц сажи для микрофотографп-ческого анализа может вызвать агломерацию частиц или каким-либо другим образом изменить их характеристики. Образование ядер сажи и их рост мало изучены. Ядра некоторых видов сажи образуются менее чем за миллисекунду после поступления горючего в пламя, и скорость образования ядер сажи, по-видимому, мало зависит от времени пребывания горючего в пламени. Механизм осаждения, управляющий образованием сажи, неизвестен.

Сталл и Пласс [15], а также Сиддел и Макграс [16] вычислили спектральную степень черноты светящихся пламен в функции объемной концентрации частиц сажи. Для этого они воспользовались теорией Ми (разд. 20.4.6), которая является результатом неносредственного применения электромагнитной теории, с целью получения радиационных характеристик сферических частиц сажи. [В результате использования теории Ми получено уравнение (21.22).] Расчеты были выполнены с использованием оптических свойств прокаленного электродного углерода при температуре 2250 К, на основании которых принимались га и х для углерода сажи. Результаты должны быть справедливы в некотором интервале температур, так как коэффициент поглощения частиц углерода в большинстве случаев слабо зависит от температуры [17].

Экспериментально было установлено, что ослабление излучения, проходящего через газ, содержащий взвешенные частицы сажи, подчиняется закону Бугера, т. е.

Jw(5) = iH0)exp(-a,5). (21.16>

В случае малых частиц, для которых я2)/Х<;0,25 (где/? - диаметр частпцы), из уравнения (20.30) теории Ми следует, что сечение рассеяния зависит от (лДД)*. Из теории Ми также следует, что в тех же условиях сечение поглощения зависит от nDlX в первой степени [см. уравнение (21.22)]. Таким образом, рассеяние пренебрежимо в сравнении с поглощением и а^ в (21.16) фактически является коэффициентом ноглощения, а не коэффициентом ослабления, определенным в уравнении (13.13). Тогда как следствие (17.44) спектральная степень черноты изотермического светящегося объема газа определяется в виде

e = l-exp(-a,L,), (21.17)

где he - средняя длина луча для данного объема.

Экспериментальные поправки к спектральному коэффициенту поглощения сажи. В некоторых случаях было определено относительно простое эмпирическое соотношение для а^, имеющее вид

а^СкГ -, .(21.18)

где С - объемная концентрация сажи (среднее значение объема частиц в единице объема облака частиц), а /с - константа. В представленных здесь численных результатах X всегда приводится в микронах. В инфракрасной области для X, меньших 0,8, Хоттель [18] рекомендует соотношение

(21.19)

В более поздних экспериментах Сиддела и Макграса [16] также было обнаружено, что соотношение (21.19) приближенно справедливо. В интервале значений 1 от 1 до 7 мкм они приводят следующие средние значения а;

Таким образом, показатель степени 0,95, предложенный Хоттелем, по-видимому, приемлем.

В работе [16] были также подробно проанализированы экспериментальные данные с целью выявления зависимости а от Я, которая обеспечила бы более точную поправку, чем постоянное значение а. Иногда а можно представить в виде

а = Cl С2 In X,

где Cl и С2 - положительные постоянные. На фиг. 21.6 приведены примеры таких зависимостей. В других случаях для представления а в функции от X требуются полиномы более общего вида <фиг. 21.7). Обобщением (21.19) для инфракрасной области спектра является зависимость вида

(21.19а)

а а = const является только приближением.

Некоторые специальные проблемы, переноса излучения 1,1

X, мкм

Фиг. 21.6. Экспериментальные значения показателя степени а в зависимости от длины волны Я для случаев почти линейной зависимости а от In Я [16]. О, □ сажа амилацетата (два различных образца); v сажа бензола; Д сажа мазута.

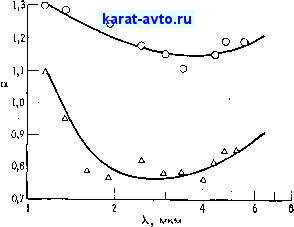
1Фиг. 21.7. Экспериментальные значения показателя степени а в зависимости от длины волны X, когда а не является линейной функцией In X [16]. О сажа бензола; Д сажа керосина.

Путем анализа экспериментальных данных, проведенного Хоттелем [18] для видимой области спектра, получена зависимость

ах = -, (21.20)

справедливая для области длин волн относительно X = 0,6 мкм (скажем, для X от 0,3 до 0,8 мкм).

Расчет спектрального поглощения сажи с помощью электромагнитной теории. Попытаемся с помощью электромагнитной теории [15, 16, 19, 20] определить коэффициент ноглощения облака частиц сажи, исходя из более общих положений. Запишем коэффициент ноглощения в виде

а, = EUN.

(21.21)

Произведение Е^А - спектральное сечение поглощения, определенное таким же образом, как и сечение рассеяния в (20.5); N - число частиц в единице объема; А - проекция площади поперечного сечения частицы (если частицы сферические, то А = я£/4); Ех - спектральная эффективная поглощательная способность, равная отношению спектрального сечения поглощения к действительному физическому сечению частицы. В области частиц малых размеров с помощью уравнений Ми для поглощающих сферических частиц малого размера получено выражение для Ех в виде

24лР

X [( 2 х2) + 2р + 4п2х2.

(21.22)

где га и и - показатели преломления и поглощения вещества сферических частиц, когда комплексный показатель преломления определяется в виде п = п - ш. Так как оптические величины га и и являются функциями %, то уравнение (21.22) можно записать следующим образом:

24яО

F{k).

(21.23)

Тогда из уравнения (21.21) следует

a, = F(K)AN = F{K),

(21.24)

где С = NkD/Q - объем, занимаемый частицами в единице объема облака частиц. Отношение

36л г, / Л ч Збя

(21.25)

является теперь функцией длины волны и может быть вычислено, если известны оптические свойства сажи в функции от X.

В работе [20] были измерены оптические свойства га и х прессованной пробы пропановой сажи. Полученные результаты приведены в таблице.

С помощью этих данных по уравнению (21.25) были вычислены значения aJC, представленные на фиг. 21.8. Хотя, как и следует из уравнения (21.18), отношение ах/С уменьшается с увеличением X, очевидно,что ири аппроксимации этой зависимости прямой линией (в логарифмических координатах) будут получены показатели степени при X, несколько отличающиеся от соответствующих показателей степени в уравнениях (21.19) и (21.20).

Теперь можно более подробно исследовать в инфракрасной области спектра вид зависимости а {X), полученной с помощью теории Ми (уравнение (21.19а)]. Приравнивая выражения (21.19а) и (21.24), получим

- = F{X). (21.26)

Принимая в этом соотношении X = i, определим постоянную к^, соответствующую инфракрасной области спектра,

h = 3QnF{i), Д21.27)

f J-1 I I I l-L.

0,4 0,6 0,8 1

6 10

Фиг. 21.8. Отношение спектрального коэффициента поглощения к объемной концентрации для сажи пропана [20].