т

полное давление смеси и парциальное давление рассматриваемых излучающих компонентов. Номограммы 6g для углекислого газа были приведены на фиг. 13.11. В .этой главе представлены более подробные номограммы для COj и водяного пара (фиг. 17.11 и 17.13). Нолюграммы для сернистого ангидрида, аммиака, окиси углерода, метана и ряда других газов можно найти в [2].

При расчете потока излучения, падающего на поверхность А, с использованием соотношения (17.59)

Qi = qiA = AegOn (17.61)

сначала по табл. 17.1 или соотношению (17.57) определяют среднюю длину пути луча для определенной конфигурации объема

Па-м

0,003

1000

1500

Tg, К

2500

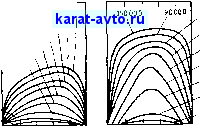
Фиг. 17.11. Интегральная степень черноты углекислого газа в смеси при полном давлении 0,101 МПа (1 атм) [1].

газа. Затем по известным значениям парциального давления газа и его температуры по фиг. 17.11-17.15 определяют степень черноты газа. На фиг. 17.11 приведена интегральная степень черноты СО2, полученная экспериментально для смеси с непоглощаю щими газами, когда полное давление смеси составляло 0,101 МПа (1 атм), а парциальное давление COg изменялось. Пунктирными линиями показаны области значений 6g, не подтвержденные экспе-

2,0 1,5

1,0 8 0,8 0.6 0,5 0,4

Ь,005 0,008 0,01

0,02 0,03 0,05 0,08 0,1 Р, МПа

0,2 0,3 0,5

17.12. Поправка на давление к интегральной степени черноты СО при значениях Р, отличающихся от 0,101 МПа (1 атм) [1]. СОг - поправка на давление; Р - полное давление смеси газа.

0,01 0,009 0,0 Ой 0,007

Фиг. 17.13. Интегральная степень черноты водяного пара в предельном случае нулевого парпиального давления в смеси при полном давлении

0,101МПа (1 атм) [1].

риментальными данными. При полном давлении смеси, отличающемся от атмосферного, следует использовать поправку на уши-

о 0,1

-\-1 \ г

PHjOe.na-m 3ju

isooo .

30000

0,04 0,06 0,08 0,10 0,12

Фиг. 17.14. Поправка на давление к интегральной степени черноты водяного пара при значениях Рн90 Г, отличающихся соответственно от О и 0,101 МПа

(1 атм) [1]:

Cjjo - поправка на давление; (Р + РНаО/ - среднее давление.

рение за счет давления [1], которая представлена в виде поправочного коэффищ1ента Ссог (фиг- .17.12). В случае водяного пара

1-г

150000 90000 МООО 45 000 30000 - 22000 15000

60000 45000 30 ООО

ггооо

15009 9000

6000

0,2 0,4 0,6 0,8 1,0 о 0,2 0,4 0,6 0,8 1,0 О 0,2 0,4 0,6 0,8 1,0

РнгоДсо+Рнго! а 6 6

Фиг. \1ЛЪ. Поправка к интегральной степени черноты в случае перекрывания полос, когда в смеси присутствуют.СОг и водяной пар [1]. а - температура газа Tg = 400 К; 6 - температура газа Tg = 813 К; в - температура газа Tg 1200 К; Д£ - поправка на перекрывание полос.

степень черноты более сложным образом зависит от парциального давления водяного пара и полного давления смеси. Значения

4 = <[б52-

(17.63)

Величина a.g{Ti) - поглощательная способность газа относительно излучения, испускаемого стенками при температуре Гц,. Эта ве.личина зависит от температуры стенки Tw, носко.тьку последняя определяет спектральное распределение излучения, поглощенного газом. Согласно fl],.величина аg может быть определена из соотношения

(17.64)

где

С02 =

0,65

асо2-+ Н20 -Аа, ССО26СО2 [~тГ~)

> = Сн

206Н2О

0,45

(17.65)

(17.66)

(17.67)

1пенями

черноты £с02 и бнгО, определенными на фиг. 17.11 и 17.13 при

аН20 =

Аа = (Аб)при т„,.

Величины бсог и бноо являются соответственно степенями

степени черноты на фиг. 17.13 с помощью множителя, зависящего от рнгО и РигОй) приведены к предельным значениям, соответствующим близкому к нулю парциальному давлению рнго в смеси, полное давление которой Р = 0,101 МПа (1 атм). Для учета действительных значений парциального н полного давлений на фиг. 17.14 приведен поправочный коэффициент СнаО- Если в смеси газов присутствуют одновременно и GOj и водяной нар, то нужно дополнительно включить в расчет величину Д^, учитывающую уменьшение степени черноты вследствие перекрывания спектральных полос ног.чощения COg и HjO. Эту поправку можно у)пределить по фиг. 17.15. Тогда степень черноты смеси GO2 и водя-яого пара в неног.лощающем газе определяется соотношением

6g = Cco26co2 + CH2oGH20--A6. (17.62)

[7.6.2. Теплообмен излучением между объемом газа и граничной поверхностью

Хоттель [1] разработал простой приближенный метод расчета ля случая, когда охлаждаемая граничная поверхность черная, температура ее такова, что поверхность испускает заметное 1злученпе. Интегральный ноток результирующего излучения, отво-г1мый от стенки, должен быть равен потоку энергии от какого-кибо внешнего источника тепловыделения, например потоку тепла, рбразующегося при сгорании газов. Если составить тепловой Цланс для газа, то оказывается, что средний поток результирующего излучения, отводимый от стенки, равен потоку собственного излучения газа за вычетом излучения от стенки, которое погло-щается газом, а именно

7ц, И соответствующих параметрахрсогL,e{TjTg)ирщо Le {TITg). Более подробная информация содержится в работах [1, 2].

ПРИМЕР 17.2. Резервуар с охлаждаемыми стенками, имеющий форму прямого кругового цилиндра диаметром 1,22 и длиной 1,22 м, заполнен горячим газом при полном давлении 0,101 МПа (1 атм). Внутренняя поверхность резервуара черная. Газ состоит из двух компонентов: прозрачного газа при парциальном давлении 0,076 МПа (0,75 атм) и углекислого газа. Смесь хорошо перемешана и имеет температуру 1110 К. Какой тепловой поток нужно отвести от стенок резервуара, чтобы сохранить их температуру неизменной, если охлаждение стенок достаточно интенсивное, так что нужно принимать во внимание лишь из.лучение газа?

Газовый объем представляет собой прямой круговой цилиндр конечной длины. Нужно вычислить поток излучения от газа к стенкам. Излучение от охлаждаемых стенок пренебрежидю мало. Используя таблицу 17.1, найдем значение длины пути луча, в данном случае Le = 0,60 Z) = 0,732 м. Парциальное давление СО, равно 0,0252 МПа (0,25 атм), поэтому рсог L = 0,0252 -0,732 = = 0,0184 МПа-м. Согласно фиг. 17.11, бсог (рсог е, g) = = 0,13, а значение Ссоа, определенное по фиг. 17.12, равно 1,0, так как полное давление смеси равно 0,101 МПа (1 атм). Предполагая, что стенки резервуара столь хо.лодные, что их из.лучение пренебрежимо мало, по соотношению (17.61) рассчитаем поток тепла, который следует отвести:

Qi = cojTgA = 0,13.5,729 Ю (1110)- 2,23л = 78,8 кВт.

17.7. ОПРЕДЕЛЕНИЕ ИНТЕГРАЛЬНОГО ПОТОКА

ИЗЛУЧЕНИЯ В ЗАМКНУТОЙ СИСТЕМЕ ПУТЕМ СУММИРОВАНИЯ СПЕКТРАЛЬНЫХ УРАВНЕНИИ

Приближение средней длины пути луча, использованное в предыдущем разделе, относилось к излучению от объема газа ко всей черной граничной поверхности или части ее, а также к осредненным характеристикам тенлообмена между газом и черной изотермической граничной поверхностью. В случае более общего анализа излучения в замкнутой системе следует рассматривать интегральный теплообмен излучением между различными парами участков граничной поверхностп, имеющими разные температуры. При этом нужно проинтегрировать уравнения теплообмена излучением, содержащие величины т^ и а^, по всем длинам волн. Для иллюстрации необходимости в подобном интегрировании бы.л приведен пример 17.1, где рассмотрена система из двух пара.ллельных шластин.

Форма спектральных уравнений задается соотношением (17.20), которое связывает плотность монохроматического потока излуче-

ния черного тела при температуре газа и плотности монохроматических потоков результирующего излучения dqi в бесконечно малом интервале длин волн для каждой поверхности. При нахождении реи1ения с учетом спектральных эффектов, как и в случае замкнутой системы тел, заполненной непоглощающей средой (разд. 10.3), для ка;кдого значения д.липы волны решается система уравнений относительно dqi (в нредположеш1И, что температуры поверхностей заданы) и затем производится интегрирование по всем длинам волн. В практических задачах об излучении газов зависимость их свойств от длины волны имеет такой нерегулярный характер, что интегрирование по всему спектру x становится практически невозможным. Это заставляет обратиться в расчетах к полосам, расположенным в огрг.личенном интервале длин волн.

17.7.1. Уравнения для полос

Приближенный подход, который ьюжно использовать для пнтегрирования уравнений по длине волны, состоит в том, что спектр разбивается на поглощающие и непоглощающие полосы. Интегрирование (17.20) в пределах типичной полосы Д>. дает

Д>. j=l.

(17.68)

= J У^ \.ihi - Fh-jri, ft-y) eib, у -F-ya, u-jeib. g] dl.

m j=l

Теперь предположим, что полосы достаточно узкие, так что

величины dqi,j, k.n-j, я, л-у, еяь./иехь, можно считать

постоянными в преде.лах ширины каждой по.лосы и отнесенными к некоторой средней длине волны в пределах этой полосы или, в случае т и а, осредненными по полосе (разд. 17.7.2). Тогда для полосы / уравнение (17.68) можно записать в виде

= 2 [iiJ - Fh-jT:i,h-j)eibj-Fk-jaik-jeib,g]Al. (17.69) 3=1

В области спектра, в которой газ практически не поглощает, Т/=1, аг = 0, поэтому (17.69) принимает вид

S (jf7P-T)J=I i8,j-F,-j)eib,jM (17.70) j=i 3=1

и совпадает с уравнением (8.19).