
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 [ 86 ] 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248
не происходит Векторная диаграмма токов для этого случая приведена на рис 10-11, (Э Из нее находим /д, = 1 А
4 Если дополнительно разомкнуть рубильник 3, то потенциалы точек п и становятся различными Сопротивления в фазах S и С получаются соединенными последовательно На каждое из этих сопротивлений приходится половина линейного напряжения Uq На топографической диаграмме точки п и а располагаются на середине отрезка ВС (рис 10-11, е)
Из топографической диаграммы находим напряжения между нейтральными точками N п между разомкнутыми концами фазы А
-63,5 В, [/д^= 2 [/дд,= 190,5 В.
Напряжения на резисторах и уменьшаются в = рач, во
столько же раз уменьтнаются токи в этих сопротивлениях = /( = 13/2 А. Векторная диаграмма токов для этого случая показана на рис. 10-11, ж.
1а

Рис 10-12
5 При замкнутых рубильниках / и 2 разомкнутом рубильнике 5 потенциалы точек А, а я п одинаковы (рис 10-11, з) Напряжения на резисторах и г^, равны линейным напряжениям [/ = t/g и [/ = Uqj. Вследствие этого токи и 1 в /3 раз больше, чем в симметричном режиме, т е /д- = А Ток /д находим из векторной диаграммы (рис 10-12, и) /д == - (/д + /с)> /д=ЗА
Пример 10-2. Три одинаковых резистора соединены треугольником (рис 10-12, а) К зажимам А, В и С приложены симметричные линейные напряжения, равные 220 В, которые не меняются при отключении рубильников 1 я 2 и изменении нагрузки При замкнутых рубильниках / и 2 линейные токи/j, = 1 А
Требуется построить топографические диаграммы цепи и векторные диаграммы токов для следующих режимов ,
1 Симметричный режим (рубильник 1 п 2 замкнуты).
2 Рубильник 1 разомкнут, а рубильник 2 замкнут.
3 Рубильник 2 разомкнут, а рубильник / замкнут
4 Рубильники 1 w. 2 замкнуты и активное сопротивление в фазе be заменено равным по ветичине емкостным сопротивлением
Решение 1 Для симметричного режима топографическая диа1 рамма цепи и векторная диаграмма гоков показаны на рис 10-12, б и е Гоки в фазах приемника в / 3 раз меньше линейных токов 1аь~ he - 1са~ l/1/З А Векторы фазных токов lb, he ha совпадают по направтению с векторами напряжений l)ab< и be и (активная нагрузка) Линейные токи определяются как разности фазных токов
Uah~ka, Ы'Ьс~ь', С са - Ьс-
2 при разомкнутом рубильнике 1 ток / = О Потенциал точки Ь' одинаков с потенциалом точки С Токи [ ь и ha остаются без изменения, поэтому прежнее значение имеет и ток /д= / - / Токи / и изменяются =--/
и Д = ка
Векторная диаграмма токов приведена на рис 10 12, г
3 При разомкнутом рубильнике 2 и замкнутом рубильнике / сопротивления в ветвях са и аЬ соединены последовательно На каждое из этих сопротивлении приходится половина линейного напряжения Ui, На топографической диаграмме (рис 10 \2 д) точка а располагается иа середине отрезка be Напряжение между разомкнутыми концами фазы А
UAa = Uj,jco% 30° = 220 ]/3/2 = 190,5 С.
Напряжения на сопротивлениях ветвей са и аЬ по сравнению с симметричным режимом уменьшаются в 2 раза Во столько же раз уменьшают токи в этих ветвях ка ~ кь ~ - 0,289 А Токи и /находим по векторной диаграмме
(рис 10-12, е)
1с = ка-ке; 1в = кс-к.ь\ /с = Д = 0,866 А.
4 Топографическая диаграмма цепи та же, что и в первом случае Векторная диаграмма токов приведена на рис 10-2, ж Из нее находим /д = 1 А, =
= 2/cos75°-=2(l/(/3)0,259=0,299 А, /,=2/ cos 15°=2 (1/(3) 0,966= 1,15 А
Пример 10-3. Определить, во сколько раз изменятся линейные токи, если резисторы предыдущего примера (рис 10-12, а) соединить звездой и включить на те же линейные напряжения (схема звезды без нейтрс1Льного провода)
Решение В схеме треугольника резисторы находились под линейным напряжением U и токи в них были I J\ 3 В схеме звезды резисторы находятся под напряжением Ujyi и, следовательно, токи в них уменьшаются в УЗ раз и станут равными / ,/3, где /, -- прелшее значение линейного тока В схеме звезды токи в линии и фазах приемника одинаковы, таким образом, линейные токи в схеме звезды в 3 раза меньше линейных токов в схеме треугольника
10-5. Расчет симметричных режимов трехфазных цепей
Для ознакомления с расчетами симметричных режимов рассмотрим порядок расчета токов в симметричной цепи рис. 10-13 Пусть напряжения на зажимах источника питания симметричны и заданы и пусть известны сопротивления всех элементов цепи 1, 2,3 и4 Для выполнения расчета проще всего преобразовать схему, заменив соединения треугольниками источника Питания и элементов 4 На соединения звездами .Сопротивления фаз симмётричшЖ^вездьГ
в 3 раза меньше сопротивлений фаз эквивалентного симметричного треугольника. Фазные напряжения эквивалентного источника питания, соединенного звездой, в j-S раз меньше заданных линейных напряжений. Таким образом, получим схему, показанную на рис. 10-14.
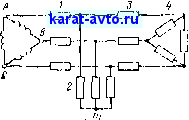

Рис. 10-13.
Рис. 10-14.

Рис 10-15.
Все нейтральные точки в симметричном режиме имеют одинаковый потенциал. Поэтому, не нарушая режима схемы, соединим их проводом без сопротивления (показан пунктиром). Затем удалим из схемы две фазы, например Б и С, и перейдем к схеме по рис. 10-15. Это не изменит режима оставшейся фазы А.
Действительно, уравнения, составленные по законам Кирхгофа, для узла А' и для контуров AAn-N и А'п^п^А' для схем, показанных на рис. 10-14 и 10-15, одинаковы, а следовательно, токи и напряжения в фазе А обеих схем также одинаковы. Токи в фазе А легко рассчитываются по однофазной схеме (рис. 10-15), например, методом ее дальнейшего преобразования - заменой параллельного соединения ветвей An, мАпх эквивалентным сопротивлением. Токи в фазах Б и С по модулю такие же, что и в фазе А. Токи в ветвях треугольника 4 в Уъ раз меньше токов в элементах 3 (в каждом из элементов любой из групп ток сдвинут по фазе по отношению к токам в других элементах той же группы на равные углы ±120°).
Для расчета симметричных режимов в сложных разветвленных трехфазных цепях широко применяют моделирование соответствующих однофазных схем.
10-6. Расчет несимметричных режимов трехфазных цепей со статической нагрузкой
При расчете симметричных режимов трехфазных цепей двигатели можно заменять эквивалентными схемами, состоящими из трех одинаковых сопротивлений, соединенных звездой или треугольни--JШM Jlaдeняя JЩшpяжшия в фaмxJШЩaтщ) сак на1тряжения 11а Трех бдинаковы^Г^сЩШивлениях: