Это соотношение известно как закон Стефана - Больцмана, в котором о - постоянная Стефана - Больцмана. Экспериментальное значение о немного отличается от вычисленного но уравнению (2.22) (табл. А.4),

ПРИМЕР 2.4. Иучок лучей, испускаемых в направлении нормали к поверхности абсолютно черного тела, несет энергию, приходящуюся на единицу площади и единицу телесного угла, 9456 13т/(м*-ср). Какова температура поверхности тела?

Полусферическая интегральная поверхностная плотность потока излучения и интегральная сила излучения в нормальном направлении связаны соотношением = леьп- Поэтому из уравнения (2.23) находим f = (ne;;,nMV4 4 (9456я/5,729.10- )V* = = 848 К. В расчете было использовано экспериментальное значение постоянной Стефана - Больцмана.

ПРИМЕР 2.5. Полусферическая интегральная новерхностная плотность потока излучения абсолютно черного тела равна 6304 Вт/м^. Какова температура поверхности тела? На какую длину волны приходится максимум спектральной поверхностной плотности потока излучения?

Температуру черного тела находим из закона Стефана - Больцмана

1/4 /. 6304

Т = {еь1ву

\ 1/4

1-8; -

V 5,729-10

Затем из закона смещения Вина находим

2,8978-10-3

576 К.

макс - Сз/Г - -

= 5,04-10-6 и =5,04 мки.

Как следует из уравнения (2.5), спектральная интенсивность излучения абсолютно черной поверхности ib (Я) не зависит от направления излучения. Эта независимость от направления, конечно, не изменяется при интегрировании по всем длинам волн. Интенсивность излучения поверхности воспринимается глазом как яркость . При рассмотрении иод любым углом абсолютно черная поверхность имеет одну и ту же яркость.

2.4.10. Максимальная интенсивность излучения в зависимости от температуры

Интенсивность излучения, соответствующая данной длине волны, определяется из закона спектрального распределения энергии Планка. Интересно отметить, что подстановка в уравнение (2.12) длины волны из закона смещения Вина [уравнение (2.17)] приводит к следующему выражению:

максЬ

С% (е

,С2/Сз

(2.24)

Из этого выражения следует, что максимальное значение интенсивности излучения увеличивается иронорционально температуре в пятой степени. В самом деле, поскольку, согласно (2.12), ihJT является функцией только ХГ, совершенно очевидно, что если температура абсолютно черного тела меняется от до Г а длины волн Я,! и %2 в те же моменты времени выбираются таким образом, чтобы = то величина ixhlT остается постоянной. Следо-

вательно, интенсивность излучения, соответствующая Яг при температуре Т^, увеличивается пропорционально пятой степени температуры по сравнению с ее величиной, соответствующей при температуре Г^. В этом основной смысл закона Вина.

2.4.II. Излучение абсолютно черного тела в интервале длин волн

В соответствии с законом Стефана - Больцмана нолусфериче-ск&я/ интегральная новерхностная плотность потока излучения

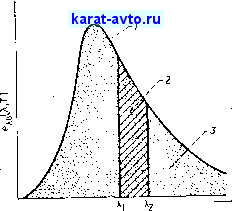
Фиг. 2.8. Энергия излучения, испускаемого в полосе. *ХЪ ) - полусферическая спектральная поперхностная плотность потока излучения; t, - длина волны; 1 - распределевтс для абсолютно черного тела при температуре Т; 2 - полоса излучения в интервале длин волн xi - Хг, 3 - излучение, соответствующее площади под всей кривой (огг*).

абсолютно черного тела находится из выражения

еь= J exh{X)dK = aT\ о

При расчете теплообмена излучением часто бывает необходимо определить долю полусферической интегральной поверхностной плотности потока излучения, испускаемую в полосе спектра (фиг. 2.8). Эта доля, обозначаемая Р^-х^, определяется соотно-

Фиг. 2.9. Физический смысл функции F. Q-Xl и™ о-ИГ - отношение заштрихованной площади ко всей затененной площади; а - кривая для определенной температуры (площадь под кпивой пяпня nTv л v no Гяповепхо Р^ ХИ-. ?) - пол?сГ;и?е^с^;я Г.Ц^

пая поверхностная плотность потока излучения; (X, г)/Т= обобщенная координата-длина волны; Л Т - произведение длины волны на температуру.

-= 5е (Я)йЯ. (2.25)

I ей (к) dX М

Последний интегра.л в уравнении (2.25) можно представить в виде двух интегралов, которые берутся от Я = 0:

Fii-i2 = [l е,ь(Я)ЙХ-J e,ft()dl] = io-X2-o-Xi. (2.26) о о

Долю интегральной поверхностной плотности потока излучения для любого интервала длин волн можно, таким образом, найти по известным величинам Fq-x в функции к. Значение функции Fo-xi (фиг. 2.9,а) равно заштрихованной площади под кривой, деленной на всю (затененную) площадь под этой л^е кривой.

Благодаря простому виду зависимости между полусферической спектральной поверхностной плотностью потока излучения и спектральной интенсивностью излучения [(2.86)] абсолютно черного тела функция ixi-X2 определяет также долю интенсивности, приходящуюся на интервал к^ - к^. Так как е^ь зависит от температуры, то для использования соотношения (2.26) понадобилось бы составить таблицы значений F-x для каждого значения Т. Однако, оказывается, что вполне достаточно иметь функцию F только от Одной переменной кТ (фиг. 2.9,6). При этом получается универсальная совокупность величин F, нримени.мая ко всем температурам и длинам волн. Универсальный вид зависимости можно найти, иеренисав уравнение (2.26) в следующем виде:

d(kT)

- Fq-XzT- Fq-

0-XiT-

(2.27)

Как видно из уравнения (2.12), величина eJT является функцией только кТ, поэтому и подынтегральные выражения в уравнении (2.27) будут зависеть только от одной неременной кТ. Значения Fq xt приведены в табл. А.5, а график зависимости /о-хт от кТ - на фиг. 2.10.

Имеются также и более подробно составленные таблицы значений Fq it для тех случаев, когда требуется большая точность. Таблицы Пивовонского и Нагеля [7], например, составлены для очень широкого диапазона значений кТ с интервалом 10 мкм-К.

Функции излучения абсолютно черного тела содержатся также в работах [8, 9].

В приложении А также приведен ряд приближенных выраже-

0,2 . 0,4 0,6 0,8 1 2

XT, мкм-К

6-10

Фиг. 2.10. Доля интегральной поверхностной плотности потока пзлучеппя

абсолютно черного тела в интервале О - Л Г. О-ЯГ ~ WiZi интегральной поверхностной плотности потока излучения; - произведение длины волны на температуру.

Как показывают следующие примеры, величины /o-;ir могут найти применение в ряде случаев.

ПРИМЕР 2.6. Абсолютно черное тело излучает при температуре 2778 К. С помощью некоторого приемника излучения нужно измерить интегральное излучение. Этот приемник поглощает все излучение в диапазоне длин волн от 0,8 до 5 мкм, но не чувствителен к излучению вне этого диапазона. Какую поправку (в процентах) долн;ен внести экспериментатор в результаты измерений энергии? Если бы имелась возможность расширить диапазон чувствительности измерений приемника на 0,5 мкм только с, одной стороны, то на какой границе выгоднее это сделать?

Так как К^Т = 0,8-2778 = 2222 мкм-К и Х^Т = 5-2778 = = 13 890 мкм-К, то доля энергии, приходящаяся на невоснрини-маемый диапазон спектра, составит /o-?.ir -Ь Р^т-оо = о-х^т + 4 (1 /?о->.,г) = 0,1050 + 1 - 0,9621 = 0,1429, т. е. ошибка будет равна 14,3% интегральной энергии падающего излучения. Расширение диапазона чувствительности измерений в сторону более длинных волн мало повлияет на точность результатов, так как кривая зависимости F от кТ в этой области имеет малый наклон. Смещение же границы в сторону более коротких волн заметно увеличит воспринимаемую энергию.

ПРИМЕР 2.7. Имеется приемник энергии излучения, который может быть чувствителен только в пределах интервала 1 мкм для всех длин волн. Экспериментатору нужно измерить интегральную поверхностную плотность потока излучения двух абсолютно черных тел - одного при 2778 К, а другого при 5556 К. Он собирается использовать интервал 1 мкм для измерения энергии излучения в полосах по 0,5 мкм с каждой стороны от максимума поверхност-вой плотности потока излучения абсолютно черного тела. От какого абсолютно черного тела воспринимается большая доля поверх-гяостной плотности иотокв излучения? Какая доля (в процентах) интегрально!! поверхностной плотности потока излучения воспринимается в каждом случае?

Согласно закону смещения Вина, в каждом случае положение максимума поверхностной плотности потока излучения соответ--ствует Хмакс = 2898/Г мкм. Так как при более высокой температуре интервал длин волн 1 мкм соответствует более широкому диапазону величин XT относительно максимума Хмакс? на приведенной кривой для абсолютно черного тела (фиг. 2.7), то измерения будут более точными для температуры 5556 К. Для абсолютно -черного тела при 5556 К Хмакс = 0,5216 мкм, а Х^Г = (0,5216 - - 0,5000)-5556 = 120 мкм-К. Ана.тогично Х^Т = 1,0216-5556 = = 5676 мкм-К. Доля воспринимаемой интегральной поверхностной плотности потока излучения составляет

100 (П-5676 - о-12о) = 100 (0,708 - 0) = 70,8%.

Аналогичные вычисления для абсолютно черного тела при 2778 К показывают, что в этом случае воспринимается 51,7% интегральной поверхностной плотности потока излучения.

Б табл. 2.1 приведены некоторые часто используемые значения Ро-хт- Интересно отметить, что при любой температуре точно четверть интегральной поверхностной плотности потока излучения приходится на диапазон длин волн ниже максимума кривой распределения Планка. Это соотношение, по-видимому, не имеет простого физического объяснения, и его следует рассматривать наряду