Г объект

Зеркальная поверхность

Изображение

Зеркальная

поверхность 1 Изображение 3

<t--t \ /Изображение

l \ if -объеша

Зеркальная поверхность 2

/Зеркальная поверхность 3

-,-ажение Изображение поверхности 2 поверхности 3

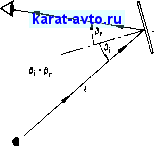
Фиг. 9.2. Траектория луча и изображения, образованные при зеркальных

отражениях.

а - изображение, образованное при однократном отражении; б - изображение, образованное при многократных отражениях; в - потоки собственного излучения от зеркальных поверхностей.

При формулировке задач по теплообмену излучением зеркальные поверхности в общем случае будут иметь ненулевую отражательную способность, т. е. они будут ослаблять энергию лучей, испускаемых объектом.

Зеркальные поверхности могут не только отражать, но и испускать излучение. Это излучение удобнее анализировать с помо-

щью системы изображений, а не системы реальных зеркальных поверхностей. При исиользовании системы изображений все излучение распространяется вдоль прямых линий, и не нужно рассматривать изменение направления при каждом отражении от поверхности. Ослабление на каждой новерхности учитывается умножением интенсивности луча на отражателную способность зеркальной поверхности при каждом отражении. Излучение трех поверхностей показано на фиг. 9.2, в. Например, излучение, испускаемое поверхностью 3, считается приходящим к наблюдателю непосредственно от изображения 3 с учетом ослабления нри отражениях на поверхностях 2 и 1, так как оно проходит через эти поверхности или их изображения.

В некоторых геометрических конфигурациях луч испытывает многократные отражения от различных поверхностей, прежде чем достигнет наблюдателя. Примером может служить система зеркал в парикмахерской, расположенных на противоположных стенах. Если эти зеркала параллельны, то луч может отражаться бесконечное число раз и человек, которого стригут, может видеть бесконечное число изображений самого себя (если зеркала совершенны, т. е. если ps = 1).

Теилообмен между простыми зеркальными поверхностями.

В качестве введения в теплообмен излучением в замкнутой системе новерхностей, часть из которых являются зеркальными, рассмотрим ряд примеров плоских поверхностей, в которых будут последовательно показаны новые особенности зеркальных поверхностей.

Собственное излучение от всех поверхностей предполагается диффузным. Это достаточно справедливое предположение для большинства случаев, что может быть показано при помощи электромагнитной теории излучения зеркальных новерхностей (фиг. 4.5).

На фиг. 9.3, а показана диффузно отражающая плоскость Ai, расположенная против зеркально отражающей плоскости А^-Поверхность 1 не может видеть себя; следовательно, обычный угловой коэффициент между любыми элементарными площадками поверхности А^ равен нулю. Однако если новерхность А 2 - зеркальная, то Ai может видеть свое изображение, и существует траектория расиространения излучения от элементарной площадки dA] к dA*f, полученная после отражения от зеркальной новерхности. Из построения хода лучей на фиг. 9.3, а видно, что излучение, нонадающее на dA* с dAi, кажется исходящим от изображения dAn2-,- Таким образом, угловой коэффициент между dAi и dA* одного отражения равен dFm-di*- Подстрочное обозначе ние относится к угловому коэффициенту между изображением dA] (как его видно на А2) и dA*.

Зеркальное и диффузное отражения имеют сходство. Когда обе поверхности А^иА (фиг. 9.3, а) - диффузные отражатели, излучение от dA, достигает dAt после диффузного отражения от Л г. Так как энергия отраженного излучения диффузно распределена.

Аг, зернамнал

. А, , изображение Аг \ %ри отражении на

У?\ ki, зеркальная

Кажущийся источник луча, падающего на Щ

Aj, диффузная-

\ 1(2) \

hx, зеркальная / \ \ \

диффузная>

А2, зеркальная

Aj, диффузная-щ^

Фиг. 9.3. Излучение диффузной поверхности на саму себя с помощью зеркальной поверхности, а - излучение между двумя элементарными площадками при одном промежуточном зеркальном отражении; б - излучение от элементарной площадки к площадке конечных размеров при одном промежуточном зеркальном отражении; в - излучение от площадки конечного размера на эту же площадку при одном зеркальном отражении; г - излучение от dA падающее только на часть А вследствие зеркального отражения от А,-

она может рассматриваться совместно с энергией собственного излучения Л 2, которая также является диффузной, и их сумма будет равна потоку эффективного излучения qoi, о чем говорилось в гл. 8. Если, однако, теплообмен между dA и dA* вследствие диффузного отражения от Л 2 исследуется отдельно от переноса энергии собственного излучения, то он описывается коэффидиентом Fax-t и затем dF-di* (не следует забывать об ограничениях, каса-югцихся однородности потока, которые вводятся при использова-

НИИ угловых коэффициентов). Часть потока собственного излучения c(?e,di-di*(2) элемента dA, которая попадает на dA* после однократного отражения от А 2, равна для случаев диффузной и зеркальной поверхностей А^ соответственно

dQe .di-di.(2) {dAieioT) Fdi-2p2dF2-di*,

dQe, dl-dl.(2)= (d4i6lOrt) p., 2 dl(2)-dl*-

Это означает, что при = ps, 2 разница в этих двух выражениях для теплообмена заключена в угловых коэффициентах отраженного излучения. Различие в угловых коэффициентах связано с геометрической природой рассматриваемого отражения.

На фиг. 9.3, б показан перенос энергии собственного излучения dAl, которое попадает на всю поверхность Ах после одного зеркального отражения. Отраженное излучение кажется исходящим от диффузно излучающего изображения dAxi)- Таким образом, угловой коэффициент между dAl и А^ равен idi(2)-i

На фиг. 9.3, в показано несколько типичных траекторий лучей, исходящих от поверхности Л X, которые отражаются обратно на А-. Эти лучи кажутся исходящими от изображения Ац)- Угловой коэффициент излучения поверхности Ai на саму себя при однократном зеркальном отражении равен Fii-i- В этом случае все изображение Ацу видно на А2, из любой точки на А^. В некоторых случаях это утверждение будет неверным. Такой пример показан на фиг. 9.3, г. Излучение, исходящее от dA, распространяется в пределах заштрихованного ограниченного телесного угла и затем отражается обратно на А-. Угловой коэффициент между dlj а Al остается равным fdi(2)-i, по зтот коэффициент относится только к части поверхности Ai, на которую падают отраженные лучи. Коэффициент Fami-i определяет видимость поверхности А^ с элементарной площадки dAn- причем видна может бытъ только часть поверхности. Этот коэффициент будет иметь разное значение в зависимости от положения dA на Ai. Тот факт, что' поле зрения между dAi и Ai изменяется с положением dAi на Air означает, что излучение, исходящее от Ai, которое отражается обратно на Ai, будет иметь неравномерное распределение по поверхности Ai. При отражении части этого излучения от А- образуется неравномерный поток излучения до от Ai, что нарушает предположение о равномерности распределения до на каждой новерхности, принятое в теории теплообмена в замкнутой системе поверхностей. Если изображение образуется на части поверхности, то должна быть проявлена осторожность при делении поверхности замкнутой системы на малые участки, обеспечивающие достаточную точность решения.

Теперь рассмотрим геометрическую систему, в которой в теплообмене излучением участвует несколько зеркальных поверхно-

2(1-21

А^, зеркальная

Аь зеркальная -У

зеркальна^! -)

Л2, зеркальная

зеркальная

Телесный угол не проходит через А г

Фиг. 9.4. Теплообмен излучением между двумя зеркально отражающими

поверхностями.

а - поток собственного излучения Аг, непосредственно падающий на dA,; б - поток собственного излучения Аг, падающий на dA, после двух отражений; в - поток соост-венного излучения А2, не попадающий на dAi после четырех отражении.

стей. Это приведет к многократным отражениям и многочисленным траекториям, по которым излучение распространяется между поверхностями. При каждом отражении излучение видоизменяется отражающей поверхностью. Вначале рассмотрим только геометрию системы; коэффициенты ps будут включены в рассмотрение позднее, когда будут сформулированы условия теплового баланса.

На фиг. 9.4 показаны две зеркальные поверхности. Излучение испускается поверхностью и падает на поверхность А^. Часть

излучения, падающая на dA, определяется угловым коэффициентом dF-di (фиг. 9.4, а). Часть излучения, попавшего на А^, отражается обратно на А^, и затем еще раз на А^. Следовательно, 2 видит dA не только непосредственно, но и благодаря изображению, образованному двумя отражениями. Это изображение построено на фиг. 9.4, б. Сначала строится отраженное изображение 1,2) объекта А-, отраженного ъ А^- Затем А^ отражается в этом изображении и получается А^а-чу Обозначение 2(i-2> понимается как изображение поверхности 2, образованное отражениями на поверхностях 1 и 2. Из рассмотрения траектории лучей и заштрихованной области на фиг. 9.4, б следует, что телесный угол, в пределах которого излучение, исходящее от А 2, падает на dA-i после двух отражений, есть тот же угол, под которым dA видит изображение Л 2 (1-2)- Таким образом, угловой коэффициент в случае двух отражений в системе равен dFa-i-ai- Это обозначение расшифровывается как угловой коэффициент между изображением поверхности 2, образованным отражениями в поверхностях 1 и 2, и элементом поверхности di.

Рассмотрим возможность дополнительных изображений. Угловой коэффициент всегда определяется путем обзора dA- с соответствующего отраженного изображения А^ через поверхность А< и все промежуточные изображения. В случае, представленном на фиг. 9.4, б, изображение поверхности А^ после четырех отражений А^ (1 2-1 2) не может видеть через А^- Следовательно, не существует луча, исходящего от А^, который попадает на dA после четырех отражений, и не требуется рассматривать дополнительные изображения.

ПРИМЕР 9.3. Бесконечно длинная канавка (фиг. 9.5) имеет зеркально отражающие стороны, которые диффузно излучают. Какая доля энергии излучения, испускаемого поверхностью А 2, попадает па элемент черной поверхности dg? Выразить результат через диффузные угловые коэффициенты излучения.

Рассмотрим сначала излучение, падающее на dA с А^ как непосредственно, так и вследствие четного числа отражений. Доля энергии испускаемого излучения, которая попадает на dAg непосредственно с А2, равна dF-dz (фиг. 9.5, а). Другая часть излучения будет испускаться поверхностью А^ на поверхность А^, отражаться обратно на и затем на dA. И-з диаграммы изображений (фиг. 9.5, б) понятно, что только часть отраженного изображения А^а-ч) может быть видна dA через А2- Доля энергии испускаемого излучения, попадающая на dA таким путем, равна угловому коэффициенту, вычисленному только по части поверхности 2(1-2)) видимой с dA, и умноженному на отражательные способности двух зеркальных поверхностей Ps, i Ps, 2 2(i-2)-d3-Это не обычный угловой коэффициент, так как он учитывает поле