Другие коэффициенты в уравнении теплообмена известны, и их подстановка дает

<?did2 = 5,73.10-41088*-700*) -(sg+--lO- (2,54-10-з)2 х

Х^Ь(Н:5 = 4,33.10- Вт.

7.4. УГЛОВЫЕ КОЭФФИЦИЕНТЫ И ТЕПЛООБМЕН ИЗЛУЧЕНИЕМ МЕЖДУ ДВУМЯ ПОВЕРХНОСТЯМИ

Одной из основных математических трудностей в исследовании теплообмена излучением между поверхностями является учет геометрических соотношений, определяющих, под каким углом поверхности видны друг другу. Эта зависимость от геометрии математически выражается в интегрировании потока результирующего излучения по поверхностям конечных размеров, участвующим в теплообмене. Было бы полезно иметь как можно больше справочных данных для учета этих геометрических соотношений для наиболее часто встречающихся геометрических конфигураций. Таким образом можно было бы избежать повторений утомительной процедуры интегрирования.

В этом разделе вводится метод учета геометрии в виде величины, названной угловым коэффициентом. Такие коэффициенты позволяют рассчитывать теплообмен излучением во многих системах с помощью формул пли табличных данных, полученных ранее для различных геометрических конфигураций поверхностей. На.ли-чие готовых формул устраняет наиболее трудоемкую и часто приводящую к ошибкам часть расчета.

7.4,1. Угловые коэффициенты для расчета теплообмена между двумя элементарными площадками

Доля энергии излучения, испускаемого элементарной площадкой черной поверхности dA, падающая на элементарную площадку черной поверхности dA, определяется как угловой коэффициент ) df Й1 й2- (Так же, как в случае уравнения (7.1), для dF будут получены те же самые результаты независимо от того, рассматривается интегральная или спектральная энергия. Интегральная

1) Угловые коэффициенты dP или dF, характеризующие перенос излучения к элементарной площадке от элементарной площадки или поверхности конечных размеров, называют элементарными угловыш! коэффициентами, угловой коэффициент Р^. характеризующий перенос излучения от элементарной площадки к поверхности конечных размеров,- локальным угловым коэффициентом, а угловой коэффициент f] 2, характеризующий перенос излучения между двумя поверхностями конечных размеров,- средним угловым коэффициентом.- Прим. ред.

энергия рассматривается здесь из сообран^ений удобства, чтобы не вводить подстрочный индекс X.) С помощью (7.3) и (7.6) приведенное выше определение можно представить в виде

dQdi -d2 oi (cos pi cos f>2/nS) dAi dA dFdi-dz = -

оТ{ dAi cos pi cos P2 J л

aTi dAi

(7.8)

где aT\dAi - интегральный ноток излучения, испускаемого элементарной площадкой dAjB пределах полусферического телесного угла. Из соотношения (7.8) следует, что dFi-di зависит только от размера dA и ее ориентации относительно dAy. Путем подстановки (7.2) выражение (7.8) можно также записать в виде

,р cos Pi dcol

(7.9)

Следовательно, все элементы поверхности dA имеют одинаковый угловой коэффициент, если они стягивают одинаковый телесный угол cfa)], иод которым они видны с элемента поверхности dA, п расположены вдоль прямой под углом относительно нормали к йЛ.

Используемая здесь система обозначений для угловых коэффициентов основана на подстрочных индексах для типов поверхностей, участвующих в обмене энергией, а обозначение в виде производной согласуется с математическим смыслом углового коэффициента. Подстрочные обозначения dl, d2 и т. д. относятся к элементарным площадкам, в то время как 1, 2 и т. д. - к поверхностям конечных размеров. Таким образом, dFdx-di обозначает угловой коэффициент между двумя элементарными площадками, как в уравнении (7.8), а dFi-dz - угловой коэффициент между поверхностью конечных размеров 4 и элементарной площадкой dA.

Обозначение в виде производной dF указывает, что рассматривается угловой коэффициент при передаче энергии к элементарной площадке, как в уравнении (7.8). Такое обозначение не требует подстрочного индекса, но сохраняет математическую форму уравнений [таких, как (7.8)], поскольку дифференциальная величина содержится в обеих частях уравнения (т. е. выражение для dF содержит элемент площади). Угловой коэффициент F относится к поверхностям конечных размеров. Таким образом, Fdi-o, - угловой коэффициент между элементарной площадкой dA и поверхностью конечных размеров А 2.

Соотношения взаимности для угловых коэффициентов между элементарными площадками. Выполнив выкладки, аналогичные тем, с помощью которых было выведено уравнение (7.8), подуча-

ем угловой коэффициент, необходимый для расчета теплообмена между двумя элементарными площадками и йА--,

J 77 cos Pl cos р2 J л

atd%~di=--o,Ai.

Разделив (7.8) на (7.10), находим обобщенное соотношение взаимности

dFai-d2 dAi = dFa2.di dA2 = --~Mi dA. (7.11)

Окончательно уравнение (7.7) для теплообмена между двумя элементарными площадками черных поверхностей может быть записано с помощью (7.11). В результате имеем

dQdin-oHn-Tl)<lFai-d2dAa {Т\-Tl)dFa2-dTdA- (7.12)

Некоторые угловые коэффициенты между элементарными пло-цадками. Ряд алгебраических преобразований позволяет свести уравнение для результирующего теплообмена двух элементарных площадок черных изотермических поверхностей к простой форме уравнения (7.12). Это стало возможным благодаря введению углового коэффициента dF, который учитывает геометрическую конфигурацию.

Вывод угловых коэффициентов будет теперь проиллюстрирован на некоторых примерах.

ПРИМЕР 7.3. Две элементарные площадки (фиг. 7.3) размещены на полосах с параллельными образующими. Вывести выражение для углового коэффициента системы dAj - dA.

Расстояние S можно представить в виде

Тогда

а гсозф Zcosroi

Телесный угол, стягиваемый площадкой й^г, под которым площадка dAi видна с площадки dA, равен

, (Площадь проекции dA) ащ =---=

(Проекция ширины dA) (Проекция длины dA) ~ ~

(/ d(p) (da:cosi))

Ыц> dx I

52 Т

cos Ц1

Фиг. 7.3. Геометрическая схема для определения углового коэффициента между элементарными площадками, расположенными на полосах, образованных параллельнызп! образующи.ми.

Подстановка в (7.9) дает угловой коэффициент системы dAi - dA , Р cos Pi dfOi I COS Ф 1 dm dx cos ю dw dx

(P+2)

(;2 + 2)3/2 n(l+xf

ПРИМЕР 7.4. Определить угловой коэффициент между элементарной площадкой и бесконечно длинной элементарной полосой, ориентированной в пространстве (фиг. 7.4) таким образом, что образующие линии dA и dAi параллельны.

В примере 7.3 выведено выражение для углового коэффициента системы элементарных площадок dA - dA, со стороной dx

тгр 1 cos ф dw dx

dFdl-d2=

Чтобы найти угловой коэффициент для случая, когда dA становится бесконечной полосой, интегрируем это выражение по х

dFdi-st2 =

Р cos ф Йф

1 cos ф

-- 00

l2Wq + 2p-=*s-) =

cos ф Йф 1 J / . ч

= -~ = -d{sm ф),

учитывая, что угол ф лежит в плоскости yz. Это полезное соотношение для углового коэффициента будет использовано в следую-ш,их примерах.

Из фиг. 7.4 также следует, что если элемент лежит на бесконечной полосе dst, i с элементами, параллельными d4st,2> то угловой коэффициент

dFdl st, 2=-2-(81Пф)

относится к независимо от положения на dst, i- Так как на полосу dAst, 2 от каждого элемента на полосе dAx

Фиг. 7.4. Геометрическая схема для определения углового коэффициента между элементарной плогщадкой и бесконечно длинной элементарной полосой: площадка и полоса имеют параллельные образующие.

падает одинаковая доля излучения, то такая же доля излучения всей полосы dst, 1 надает на dA . Следовательно, угловой коэффициент между двумя бесконечно длинными полосами элементарной ширины, имеющими параллельные образующие, должен быть равен коэффициенту системы - dAt, 2, или Vjd (sin ф). Угол ф всегда лежит в плоскости, нормальной к образующим обеих полос.

ПРИМЕР 7.5. Рассмотрим бесконечно длинную клинообразную полость, сечение которой показано на фиг. 7.5. Определим угловой

коэффициент между элементарными полосами dx тз. d% ъ функции X, I и,а.

Как показано в примере 7.4,

dFdx-di = 2 (sin = Т

Из геометрических соображений (фиг. 7.5, б)

&sin а cos ф = --j-.

Величина йф представляет собой угол, стягиваемый проекцией dl, нормальной к L;

dgcos(a-l-f) dl г sin а

L L L

Из закона косинусов имеем = -f- 2 cos а,

тогда

dFdx-di = -5-cos ф йф =

1 xlArfia,y - 2 1з 1 х1 sin а

Т(л:2 + 2 2х| cos сб)3/2

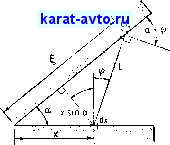
-.dl.

i, sin а

7.4.2. Угловой коэффициент между элементарной площадкой и поверхностью конечных размеров

Рассмотрим теперь элемент йЛ изотермической черной поверхности при температуре Г^, обменивающийся энергией с поверхностью конечных размеров А 2, которая также является изотермической и поддерживается при температуре Гд. Соотношения, полученные для расчета теплообмена между элементарными площадками, должны быть распространены на случай поверхности конечных размеров А^ (фиг. 7.6). На фиг. 7.6 показано (сравните сплошную и пунктирную линии), что угол р2 будет различным для разных положений на поверхности 2 и что угол и расстояние S также будут изменяться.

Рассмотрим два угловых коэффициента: угловой коэффициент di 2 между элементарной площадкой dA и поверхностью конеч-

Фиг. 7.5. Угловой коэффициент между двумя полосами на-сторонах клинообразной полости.

а - геометрия клинообразной канавки; б - вспомогательное построение.