Интенсивность падающего излучения {X, Тi) = iib {X, 1667 К). Согласно уравнению, предшествующему (3.416), интенсивность отраженного излучения равна

к (Рг=0°) = f (К го {X, Рг=o Гл) dx=

о

о *

С учетом (2.27) получаем

ir(Рг = 0) = {0,7F,.2t. + 0,2F2T.-5t. + 0,ЬРьт.-оо) = = ii. 16,67* [0,7-0,347 + 0,2 (0,869-0,347) -f

+ 0,5 (1 - 0,869)] = 58 ООО Вт/(м2.ср).

3.7. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ

В данной главе была введена строгая система обозначений и даны точные определения радиационных свойств, которые сведены для удобства в табл. 3.1.

С помощью зтих определений можно установить ограничения для различных выражений закона Кирхгофа, связывающего степень черноты с поглощательной способностью тела. Эти ограничения являются иногда источником недоразумений, в связи с чем в сводной таблице (табл. 3.2) перечислены условия, ири которых а можно заменять на Эти ограничения учитываются также ири выводе формулы £ -- р = 1 из основной формулы а -f р = 1 для непрозрачных те.л.

Приведенные подробные определения сделали возможным вывод соотношений взаимности для отражательных способностей и определение существующих ограничений. Эти ограничения перечислены в удобной сводной таблице (табл. 3.3).

Литература

1. Brandenberg W. М., The Reflectivity of Solids at Grazing Angles, Measurement of Thermal Radiation Proportie; of Solids, J. C. Richmond (ed.), NASA SP-31, pp. 75-82, 1963.

1. Спектральная степень черноты некоторого вещества существенно изменяется с длиной волны, но почти не зависит от температуры поверхности (см., например, фиг. 5.3). На поверхность зтого вещества падает излучение от серого источника с температурой Tj. Показать, что интегральная поглощательная способность падающего излучения равна интегральной степени черноты вещества при температуре источника излучения Г,.

2. Используя фиг. 5.3, оценить полусферическую интегральную степень черноты вольфрама при температуре 2800 К.

3. Допустим, что х не зависит от X (серое излучение). Показать, что Fq xt представляет собой долю интегрального излучения зтого серого тела в диапазоне О - XT.

4. Одинаково ли положение максимумов кривой распределения для некоторой поверхности с полусферической спектральной степенью черноты 6х и кривой распределения е^ъ при той же температуре? {Указание. Рассмотрите изменение deJdX.) Постройте график е^ в зависимости от X для данных, приведенных на фиг. 3.7 при температуре 55В К, и для данных, приведенных в задаче 3.6а при температуре 333 К. Какой длине волны X соответствует максимум е^? Как отличается зта величина от максимума е^ь?

5. Белая керамическая поверхность имеет распределение полу- сферической спектральной степени черноты при температуре 1667 К, изображенное ниже. Чему равна ее полусферическая интегральная степень черноты? Ответ: 0,28.

6 8 10 X, мкм

6. Поверхность при температуре 60° С (333 К) имеет следующие

значения полусферической спектральной степени черноты: /., мкм < 1 1 1,5 2 2,5 3 3,5 4 4,5 5 6 7 8 >8 €х(Х,ЗЗЗК) О О 0,2 0,4 0,6 0,8 0,8 О 8 0,7 0,6 0,4 0,2 О О

а. Какова полусферическая интегральная степень черноты поверхности при температуре 60° С?

б. Какова полусферическая интегральная поглощательная способность поверхности при температуре 60° С, если источником падающего излучения является серая поверхность (степень черноты 0,8) при температуре 1110 К? Излучение распространяется равномерно при всех углах падения. Ответы: а. 0,064; б. 0,50.

7, Направленная, степень черноты серой поверхности изображена на графике. Свойства изотропны относительно азимутального угла 0.

а. Чему равна полусферическая степень черноты этой поверхности?

б. Если поток падающего черного излучения при температуре 93° С равномерно распространяется по всем направлениям, то какая доля падающей энергии будет поглощаться этой поверхностью?

в. Если эту поверхность поместить в окружающую среду с температурой О К, то каким должен быть поток энергии, подводимой к 1 м^ этой поверхности, чтобы ее температура оставалась равной 556 К?

Ответы: а. 0,575; б. 0,575; в. 291,5 Вт.

19=0

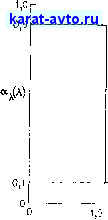
Поверхность

--SiO-AI

.Идеальная изоляция с обратной стороны

Длина Волны Л, мкк

9. Используя фиг. 5.21, найти поглощательную способность бума-ги для пишущей машинки при освещении ее по нормали светом 11 от абсолютно черного источника при температуре 1178 К.

8. Спектральная поглощательная способность aj, {У) селективной поверхности SiO - А1 может быть приближенно представлена графиком, приведенным ниже. Поверхность находится на земной орбите вокруг Солнца, и на нее в направлении нормали падает поток солнечного излучения 1393 Вт/м^. Какова равновесная температура поверхности при условии, что а?, не зависит от угла и температуры поверхности? Отеет: 665 К.

Поток солнечного излучения

11111

ОПРЕДЕЛЕНИЕ РАДИАЦИОННЫХ СВОЙСТВ С ПОМОЩЬЮ КЛАССИЧЕСКОЙ ЭЛЕКТРОМАГНИТНОЙ ТЕОРИИ

4.1. ВВЕДЕНИЕ

В 1864 г. Джеймс Клерк Максвелл опубликовал статью, в которой показал, что между электрическим и магнитным полями суш;ествует связь и что электромагнитные волны распространяются со скоростью света, а свет в свою очередь является одной из форм электромагнитных волн [1]. Эти открытия являются величайшими достижениями классической физики. Хотя, как уже было показано, перенос энергии электромагнитного излучения управляется квантовыми эффектами, можно и даже необходимо определять многие свойства видимого и теплового излучения с помощью классической волновой теории.

В этой главе будет показано, что степень черноты, а также отражательная и поглощательная способности веществ в некоторых случаях могут быть вычислены с помощью их оптических и электрических свойств. Соотношения между радиационными свойствами вещества и его оптическими и электрическими свойствами были установлены из рассмотрения взаимодействия на границе раздела при переходе электромагнитной волны из одной среды в другую.

Анализ основан на предположении об идеальном взаимодействии между падающей волной и поверхностью. В физическом смысле это значит, что полученные результаты применимы для оптически гладких, чистых поверхностей, обладающих зеркальным отражением. Распространение волны и ее взаимодействие с поверхностью будут рассмотрены в несколько упрощенном виде с помощью основных уравнений Максвелла, связывающих электрическое и магнитное поля. Используя более строгую теорию, чем применяемая здесь волновая теория, можно более точно оценить свойства для идеальных поверхностей. Однако затрачиваемые усилия чаще всего не оправдываются, так как ни в упрощенных, ни в более сложных расчетах нельзя учесть влияние качества обработки поверхности. Из-за отличия реальных материалов от идеальных, рассматриваемых теорией, экспериментальные значения величин часто существенно отличаются от предсказанных теорией. Эти расхождения обусловлены такими факторами, как

наличие примесей, шероховатость поверхности, загрязнение поверхности и изменение кристаллической структуры при обработке поверхности.

Хотя на практике состояние поверхности может оказывать большое влияние, приводимая здесь теория полезна во многих отношениях. Теория дает возможность понять причину основных различий в свойствах диэлектриков и электропроводных материа-алов, установить основные тенденции, с помощью которых удается обобщить экспериментальные данные. Эти тенденции полезно также знать при выполнении инженерных расчетов, когда приходится экстраполировать имеющиеся ограниченные экспериментальные данные на другой диапазон. Теория оказывается полезной при объяснении зависимости от угла отражательной, поглощательной способностей, а также степени черноты. Так как электромагнитная теория справедлива для чистых веществ с идеально гладкими поверхностями, она позволяет вычислить одно предельное значение, которое может иметь данная характеристика. Например, можно определить максимальное значение отражательной способности или минимальное значение степени черноты металлической поверхности.

В разд. 4.3-4.5 приводится довольно подробный вывод соотношений классической теории, которые применяются дЛя описания радиационных свойств. Окончательные результаты собраны в разд. 4.6, где также приведены примеры их практического применения. Читатели, которых интересует только, как применить полученные результаты для расчета свойств, могут пропустить разделы, содержащие выводы, и обратиться непосредственно к разд. 4.6.

4.2. ОБОЗНАЧЕНИЯ

Ci, Cj - постоянные в законе Планка распределения энергии по спектру;

с - скорость электромагнитной волны в среде, отличной от вакуума; Со - скорость электромагнитной волны в вакууме; Е - напряженность электрического поля; е - поверхностная плотность потока излучения; Н - напряженность магнитного поля; К = у/уо - относительная диэлектрическая проницаемость; п - показатель преломления; п = п - iK - комплексный показатель преломления;

Гд - удельное электрическое сопротивление; S - мгновенная скорость переноса энергии через единицу площади;