Экран

Падающее излучение

I Отверстие

т

-~Т^1!нпенсивность

,--дифрагировавшего

излучения

Фиг. 20.6. Дифракция на отверстии или сферической частице больших размеров.

а - дифракция излучения на отверстии; б - индикатриса рассеяния при дифракции на сфере большого размера.

дифракция может быть включена В перенос излучения, как если бы она являлась частью излучения, проходяш,его мимо частицы без взаимодействия с ней. Вследствие этого при рассмотрении обмена энергией в пределах рассеивающей среды дифракцией часто можно пренебречь.

Наиболее известная форма дифракции получается при прохождении света сквозь маленькое отверстие или щель. В этом случае образуется дифракционная картина из перемежающихся темных и светлых колец или полос (фиг. 20.6, а). Если сферическая частица находится на пути падающего излучения, то, согласно принципу Бабине, интенсивность дифракционных полос такая же, как и в случае отверстия. Это является следствием того, что отверстие и частица вызывают добавочные возмущения амплитуды падающей электромагнитной волны. При дифракции на сферической частице и на отверстии такого же диаметра величины энергии одинаковы. Вследствие этого в дифракционном процессе принимает участие полная площадь проекции сферы и сечение рассеяния при дифракции равно площади проекции nD/A. Поскольку дифракция и отражение происходят одновременно, то полное сечение рассеяния может быть близким к 2 (лОИ), если сфера является сильным отражателем.

Индикатриса рассеяния в случае дифракции на сфере большого размера выражается через бесселеву функцию первого рода первого порядка [1]

W; - X ) \ (лдд) sin ф j

(20.22)

Эта функция представлена на фиг. 20.6, б. Поскольку абсцисса равна (nD/X) sin ф, то для частиц с большим значением nD/X дифрагировавшее излучение заключено в пределах небольшого угла в направ.лении прямого рассеяния. Для мелких частиц с nDiX л; 1 теория, с помощью которой получено выражение (20.22), не справедлива и следует применять общую теорию рассеяния Ми. В работе [9] путем интегрирования показано, что (20.22) удовлетворяет (20.14); интегрирование следует производить лишь в пределах малого угла ф, что значительно упрощает вычисления.

20.4.5. Рэлеевское рассеяние

Во многих случаях диаметр рассеивающих частиц значительно меньше д.липы волны падающего излучения (D <Х). Рассеяние на таких частицах называется рэлеевским по имени Рэлея, исследовавшего этот случай. Рэлеевское рассеяние имеет важное значение для атмосферы, где рассеивающими частицами яв.ляются молекулы газа. Сечение рассеяния можно рассчитать с помощью

квантовой или электромагнитной теории. Первоначально Рэлей получил функциональную зависимость с помощью анализа размерностей

(20.23)

где V - объем частицы, а G (ге) - неизвестная функция комплексного показателя преломления рассеивающего вещества. Наиболее важный вывод состоит в том, что при рэлеевском рассеянии энергия излучения, рассеянного в каком-либо направлении, обратно пропорциональна четвертой степени длины волны' падающего излучения. Эта обратная зависимость показывает, что если падающее излучение охватывает некоторый участок спектра, то цутем рэлеевского рассеяния наиболее сильно рассеивается коротковолновое излучение.

Рэлеевским рассеяние.м па молекулах воздуха объясняется голубой фон неба и красный цвет солнца на закате. Голубая часть падающего солнечного света находится в коротковолновой области видимого спектра, поэтому она подвергается интенсивному рэлеевскому рассеянию во всех направленпях, и небо приобретает голубой фон. В отсутствие молекулярного рассеяния небо казалось бы черным всюду, за исключением прямого направления по солнечному лучу. Когда солнце садится, длина пути прямого излучения через атмосферу становится больше, чем в середине дня. При прохождении луча по этому более длинноагу пути часть коротковолновой области спектра, рассеиваемая в сторону от прямого пути солнечных лучей, увеличивается. В результате солнце па закате приобретает красный цвет, поскольку длинноволновые красные лучи способны проникать в атмосферу с л[епьшпм ослаблением, чем лучи в остальной части видимого спектра. В присутствии множества частиц ныли красный цвет заката становится интенсивнее.

При наличии в атмосфере частиц в очень ограниченном интервале размеров можно наблюдать необычные эффекты рассеяния. После извержения вулкана Кракатау в 1883 г. в течение многих лет наблюдался голубой и зеленый цвет солнца и луны. Этот эффект объясняется наличием в атмосфере частиц с такими размерами, нрп которых рассеивалась лпшь красная часть видимого спектра. 26 сентября 1950 г. в Европе наблюдали голубой цвет солнца и луны. Это явление было обуслов.тено присутствием в атмосфере тонко диспергированных частиц дыма одинакового размера, нрииесенных пз Канады, где горели леса.

Сечения рэлеевского рассеяния. Уравнение (20.23) определяет только функциональную завпспмость рассеянного излучения от длины волны и объема частиц; поэтому нужна дополнительная информация относительно сечений рассеяния на частицах и угло-

вого распределения интенсивности рассеянного излучения. Рассмотрим сначала мелкие, не поглощающие (х = 0) частицы, для которых п = пи nD/l < 0,6/ге, где X - длина волны в веществе частицы. Сечение рэлеевского рассеяния в случае неполяризованного падающего излучения можно рассчитать с помощью более современной теории

24.t3l2 / п^-1 \2 8 лО / лО \4 / п^-\ \2 /ОА ол\

л = -1-;) -I-) 1;) -

Часто сечения рэлеевского рассеяния выражают через поляризуемость частиц ар, которая является коэффициентом иронор-

Таблица 20.2

Поляризуемость для различных условии рассеяния

Рассеивающие частицы

Ограничения

По.шризуемость о. (дл1ша) 3

Электроны (томсо-новское рассеяние)

Частицы диэлектрика небольшого размера (рэлеевское рассеяние)

Среда, содержащая малые частицы (лоренц-лорен-цевское рассеяние)

Среда, содержащая малые частицы

Среда, содержащая малые частицы

Энергия падающих фотонов мала, hv <S mcj

Диаметр частиц мал по сравнению с длппой волны в среде н частице

Расстояние между частицами мало по сравнению с длиной волны {<Х). Диаметр частиц очень мал (О X) по сравнению с X в среде и частице. Расстояние между частицами > D

Расстояние между частицами велико (>: X). Диаметр частицы очень мал (D X)

Расстояние между частицами велико (>;. X). Дпаметр частицы очень мал (D X). п 1,0

- i-\ CJ \ 2л /

п-Ч-2 V 2 j

2-1

n-1 I )

1) <;2/4nvomgC2 = 2,818- IO-1ч см- классический радиус электрона. 2) В утом случаеИ является показателем преломления вещества частиц и зависит от концентрации частиц и объема [1].

циональности между силами, индуцированными в молекулах, и внешним электромагнитным полем. В частности, он связывает дипольный момент в единице объема веш,ества и внешнее поле.

Для рассматриваемого здесь случая поляризуемость равна

,=7 4=4-. (20.2.5)

4п п2 -2

так что выражение (20.24) можно записать в виде

В этом более общем виде выражения для сечения рэле-евского рассеяния на разных частицах могут быть получены путе.м подстановки в (20.26) соответствующих соотношений для ар. В табл. 20.2 приведены некоторые соотношения для отдельных частиц и для частиц в прозрачной среде.

Действительная зависимость от X сечения рассеяния для частиц в среде может несколько отличаться от1/А-*. Например, в воздухе нри стандартных температуре и давлении основное значение имеет рэлеевское рассеяние на молекулах газа. Однако вследствие зависимости показателя преломления от длины волны изменепие сечения рассеяния несколько отличается от зависимости Это показано на фиг. 20.7, где действительная зависимость рассеяния от длины волны сравнивается с зависимостью

Для частиц из проводящего вещества с кодшлексным показателем преломления п = п - ix выражение для сечения рассеяния имеет более общий вид, чем (20.24):

Фиг. 20.7. Сравнение действительного изменения сечения рэлеевского рассеяния в воздухе нри стандартных температуре и давлении с зависимостью ill* [6].

-С- действительное рассеяние;

----~ - сечение рэлеевского рассеяния; к - длина волны.

24я31/2

п2 + 2

~ 3 4 \ X j

п2--2

(20.27)

Подставляя п = п - in и возводя в квадрат' абсолютные величины, получим

24ЛЗУ2 [( 2 2 l)( 2 2 2)-h4nx2]2-H36 2x2 П 28

При x = О это соотношение сводится к (20.24). Величина sJ(2л^VIX), вычисленная с помощью (20.28) нри различных значениях тг и х, приведена на фиг. 20.8.

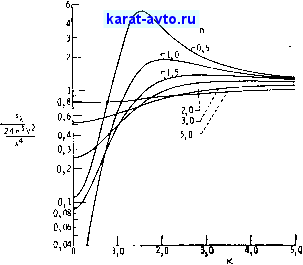
Фиг. 20.8, Сечение рэлеевского рассеяния в зависимости 6т показателя преломления п и показателя поглощения и.

Индикатриса рэлеевского рассеяния. При неноляризованном падающем излучении, согласно электромагнитной теории, индикатриса рэлеевского рассеяния имеет вид

Ф(Ф, 9)=4(l+=°Ч')

(20.29)

Это выражение не зависит от азимутального угла 9.

Графики индикатрис рэлеевского и изотропного рассеяния приведены на фиг. 20.9. При рэлеевском рассеянии ноток рассеянной энергии нанравлен в основном вдоль падающего излучения в прямом и обратном направлениях относительно источника излучения.