
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 [ 23 ] 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248

вида (2-14) вообще можно выполнить относительно любого элемента gtj, выраженного в виде некоторой суммы проводимостей. Элементы главной диагонали определителя узловой проводимости (2-13), как правило, равны суммам проводимостей соответствующих ветвей. Поэтому разложение (2-14) выполняется обычно относительно ветви, присоединенной между /-м и базисным (заземленным) узлами, с проводимостью, входящей в элемент главной диагонали (соответствующей /-й строке и /-му столбцу), которую обозначим в дальнейшем g-o = g}. При этом
где ветвь с проводимостью в общем случае остается по-прежнему присоединенной между -м и t-M (не базисным) узлами.
В этом случае вместо равенства (2-14) нужно записать;
D=g,D, + D>, (2-15)
где нижний индекс у минора первого слагаемого обозначает, что /-я ветвь закорочена, а верхний индекс у второго слагаемого указывает, что та же ветвь в той же схеме разомкнута, при этом Dj - положительное, так как проводимость g входит в элемент, стоящий на главной диагонали (алгебраическое дополнение равно минору).
Для иллюстрации применения формулы разложения (2-15) рассмотрим схему на рис. 1-22, а, для которой была записана система уравнений (1-35) относительно потенциалов ф1, фз и фз при ф4 = О и определитель (1-36):
{gi + gn + gis) -gi2 ~gl3
£)(S)= -g2i {g2+g21 + g23) -g23
- g31 -g32 (g;3 + g3i4-g32)
Разложим этот определитель относительно ветвей g, g и (рис. 2-8), присоединенных к базисному узлу 4. Проводимости gi, gfa и £з в приведенном определителе (подчеркнуты) представляют собой избыточные члены соответствующих строк или столбцов. Это означает, что при удалении такой проводимости из диагонального элемента сумма всех остальных элементов соответствующей строки и столбца равна нулю.
Рис 2-8.
По формуле (2-15) получим;
ig2+g21 +
g3i
gia) -gi2
- g21 (g2+gil+g23)
- gal -ga2 (gs
g2s) -giS
(g3 + g3l4 -gl3 - g23
f Й'зт+Ы
giDi + DK (2-16)
Полученным минору Dj и определителю соответствуют схемы на рис. 2-9, а и б. Разлагая каждый из определителей (2-16) согласно равенству (2-15) по проводимостям других ветвей, присоединенных к базисному узлу, можно получить еще более простые выражения.
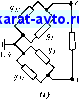
Рис. 2-9.

g2Dl + D\ (2-17)
Например, разложим определительотносительно проводимости
igii + g:3) -gi3
- g3i {g3+g3i + ga2)
(gn + gu) -gi2 -gi3
- gil (gil+gis) -gis
- g3i -gsi (§-з + Яз1+Ы
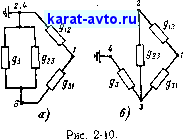
Минору Dz и определителю D соответствуют схемы, показанные соответственно на рис. 2-10, а и б. Дальнейшее разложение и по формуле (2-15) относительно проводимости g приводит к следующим выражениям:
(gl2+g-13) - gl3
- gsi (gsi + gaz)
{gl2+gl3) -gl2 -gl3
goPl = g.gz {gl2 + gl3) + g2
= g2g3Dl3 + g2D\\
Di2 =
--ga
1l2-\-glu) -gii - gil ig21-\-gi3)
- g21 {g21+g23) - g23
- gal - g32 (gsi + gs2)
.£)123
= g3Di
Аналогично можно получить разложение для первого слагаемого (2-16):
giDi=giDi + gxg2Dl + ggDl3 + gig2g3Di23. (2-18) После суммирования выражений для gDi и получается:
D(y> g,Dr + g,Di -f gM 4- gigiDl, + + g2g3Dk + gigaDn + gig2g3Di23 + D (2-19)
где D = 0 (рис. 2-11), поскольку этот определитель получается длясхемь], в которой = р„ = g., = П; минпр П^.. - 1, тк клтг-


Рис. 2-11.
Рис, 2-12.
его значение находится при gi = g2 = = °° (короткое замыкание этих ветвей).
Таким образом, каждому слагаемому (2-19) соответствует определенная схема, которая легко получается из основной схемы путем наложения условий на проводимости ветвей, присоединенных к базисному узлу.
Структура полученной формулы разложения определителя узловой проводимости (2-19) позволяет применить ее для разложения определителя, составленного для более сложной цепи.
Например, определитель (1-41) для схемы рис. 1-23, б
может быть разложен по избыточным элементам главной диагонали (по проводимостям gl, g2, ga и g) в виде
Dy>giDr+giDr +g3Dl + giDr+gigiDl + gig3Dr3 + + gigiDll + g-igaDit -f ggiDfi 4- gugiDll + gig2g3D\n + 4- gigigiDm + gig3giDl3i + g2g3giDm + gigig3giDii3i 4- /?*. (2-20)
где Di234 = 1 и Di = 0.
Каждому слагаемому этого определителя соответствует схема, полученная из рис. 1-23, б при Ji = О наложением условий на значения проводимостей ветвей, присоединенных к базисному узлу. Например, Df * находится для схемы рис. 2-12, полученной из заданной схемы при gi = оо и g2 = ga = gi = 0:
(§ 214-Ы -g23 О
DV= -ga2 (ё'зз + Ы -g3i
о -gi3 {gil+gi3)
Обобщая выражения (2-19) и (2-20), составим общее выражение для разложения узлового определителя по ветвям g, g, ... , g-, присоединенным к базисному у + 1-му узлу:
Diy) = S g.Di + Е gtgjDi, + S g,g,gkD,j, +... + gig2..-gy, (2-21)
где верхние индексы, указывающие на номера разомкнутых ветвей, опущены, поскольку одни нижние индексы определяют как закороченные, так и разомкнутые ветви. Например, слагаемое вида g,Di соответствует схеме с t-й закороченной ветвью и с разомкнутыми остальными ветвями; число таких слагаемых, очевидно, равно числу ветвей, присоединенных к базисному узлу. Слагаемые вида gig,Dii соответствуют схемам с двумя закороченными ветвями gi и g, и остальными разомкнутыми, причем число таких слагаемых равно числу сочетаний по гтвя из у проводимостей.