
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 [ 184 ] 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248
Если рубильник не включается, а отключается (рис. Ig.g задача решается еще проще. В этом случае, зная ток в размц
при
каемом рубильнике, необходимо рассчитать токи в линиях подключении источника тока противоположного знака непосред венно к концам отключаемой ветви. Токи в сосредоточенных сопп тивлениях и схемы, изображенной на рис. 19-8, г, равщ искомым токам волн в линиях.


Рис 19-9.
Таким образом, расчет волн, возникающих при переключениях, может быть сведен к расчету эквивалентных схем с сосредоточенными параметрами.
Пример 19-3. Найти волну, возникающую в линии с волновым сопротивлением Zc при подключении к ней источника с э. д се- Eq, внутренними сопротивлением г и индуктивностью L (рис 19-9, а)
Решение Составив эквивалентную схему с сосредоточенными параметрами (рис 19-9, б) и рассчитав токи волн в линии, находим для тока волнь в начале линии (х - 0) выражение, аналогичное (13-12)
r + z,
-где т
в любой точке линии при t> xh в соответствии с (19-7) ток прямой волны
пр = - =
I -е
Ток волны для этого случая показан на рис 19-9, а
Пример 19-4. Найти волну, возникающую в линии с волновым сопротивлением 2(. при подключении к ней источника с синусоидальной э д с е = sin (ю^ + ф), внутренними сопротивлением г и индуктивностью L (рис 19-9, е)
Решение Эквивалентная схема та же, что и в предыдущем примере (рис 19-9, б) Рассчитаем ток в этой схеме. р
i = [ sm (ю^ -Ь f - ф) - sm (ф - ф) е !],
где
г = у (r-f 2c)8-f coL; ф = а1с1
r + Zc
в произвольной точке линии с координатой х при t > xjv
t - xlv
sm (ю/ -0M/t)-l-ij5 -ф) -sjn (i); -ф)е
np m
Ток волны показан на рис 19-9, в.
19-5. Отрежение волны с прямоугольным фронтом от конца
линии
Отражение ст сопротивления. Рассмотрим волну с прямоугольным фронтом
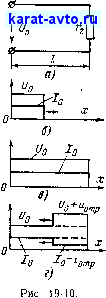
пад = о; 1ппд = /о=--Л/гс. (19-18)
движущуюся по однородной линии и падающую на приемник с активным сопротивлением (рис. 19-10, а и б). Когда волна дойдет до конца (рис. 19-10, в), она частично отразится. В рассматригаемом случае падающая волна движется в направлении возрастания X (в прямом направлении ) и может называться прямой. Отраженная волна движется в обратном направлении и может называться обратной. Однако при исследовании отражения волны удобнее пользоваться понятиями падающая и отраженная волны, а не прямая и обратная .
Для определения условий отражения волны найдем ток в сопротивлении fj.
Напряжение в конце линии щ = Ыпад + or;, а ток = i - - г„р. Поэтому ток отраженной волны tp -= - = /ц - г'г и напряжение Но-р -= отр^с = {Iq - = Ug - zj-
Тогда
2 = 212 = + отр = 2t/o - г,12, (19-19)
-u=J Ц90)
Из выражений (19-20) следует, что ток в сопротивлении г рав току, который получился бы в схеме с источником напряжеии 2t/o и сопротивлениями и г^, включенными последовательно^
Напряжение в конце линии зависит от величины и знак отраженной волны (рис. 19-10, г). Из (19-19) и (19-20) находим^
*отр
отр
отр
r, - Zr и„
-г- = /о
где п = Тогда
гг + гс
- коэффициент отражения.
2 = Л + отр = (1 + ) о;
t2 = /o-oTp=(l - ) /о-
Если линия на конце разомкнута (rg = оо), то п
(19-21) (19-22)
(19-23) (19 24) (см. также
гл. 18) и Uorp = Uo, /отр = -0. т. е. волна отражается полностью без перемены знака. Напряжение в конце удваивается: 2 = 2Uo, а ток /а = О-
Если линия на конце короткозамкнута
(Гз = 0), то я = - 1 и Нотр = - (
= - /о, Т. е. волна отражается Полностью с переменой знака. Напряжение в конце линии 2 = О, а ток /2 = 2/(.
Вообще можно сказать, что если сопротивление приемника энергии больше волнового сопротивления линии Гз > 2c, я > о, то падающая волна встречает в конце линии большее сопротивление. Ее заряды не успевают стекать через это сопротивление и напряжение в конце линии, обусловленное зарядами, приносимыми волной, возрастает, 2 = (1 + > о-Отраженная волна имеет тот же знак, что и падающая.
Если же Гз < Zc, то, наоборот, через сопротивление Гз стекает большее количество зарядов, чем приносится волной; требуется дoпoлJ нительное поступление зарядов из заряженной линии, что приводит к снижению напряжения в линии. Отраженная волна имеет знак, противоположный знаку падающей, и на конце линии напряжение понижается.
Если Гз == Zc, то я = О, Но-гр = О, /отр = О и'отраженной волны нет. Как только волна дойдет до конца, в цепи сразу установится неизменный ток, и вся энергия, доставляемая падающей (бегущей) волной, поглощается в сопротивлении г^.
При падении отраженной волны на начало линии она должна р-асе^.атриватье?т ат-назющаяу дви?кущаяея-в- об&атном и jp