
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 [ 171 ] 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248
группируя члены в правой части и вводя гиперболические функции chy X и sh у X, будем иметь: .. .
I = -2 -2-+ -1--= ~ -/shyx + Zichyx.
(18-21)
Эти формулы позволяют определить ток и напряжение в любой точке линии по их значениям в начале линии.
Пусть теперь заданы значения напряжения и тока Д в конце линии, т. е. задан режим приемника, а значит, и сопротивление
В этом случае целесообразно отсчитывать расстояние текуПгей точки от конца линии. Обозначая его через х\ получаем х = / - х', где / - длина всей линии.
Тогда из (18-7) и (18-12) найдем:
Обозначим
и условимся, отсчитывая расстояния от конца линии, обозначать их не через х', а снова через х. При этом никакой путаницы внесено не будет, так как в каждом конкретном случае по заданным напряжениям и токам Cj, Д или 0-2, Д видно, откуда отсчитываются расстояния. Тогда
и = АфУ^ + А^е-\ lZc=-Ke~A у^, (18-22)
где АдеУ - прямая волна напряжения, а А^е'У - обратная волна. Из формул (18-22) при х = О получим:
4=(f/2 + W; А,= 1 iU2~i2Zc). (18-23)
Подставляя (18-23) в (18-22), группируя члены и вводя гиперболические функции ch ух и sh ух, получаем:
(jljchуж + Дг,sh ух;
и
/ = sh ух 4- 2 ch ух.
(18-24)
К формулам (18-24) относятся все замечания, сделанные выше относительно формул (18-21).
Соотношения для линий постоянного тока, у которых сопротивление проводов и утечка между проводами, обусловленная [есовершенством изоляции, равномерно распределены вдоль линии, Ьэгут быть патучены как частный случай из выведенных соотношений (18-24) при со = 0. В самом деле, со = О означает, что при
постоянных во времени токах и напряжениях отсутствуют э. д самоиндукции (но не магнитное поле между проводаги) н'хо смещения между проводами (но не электрическое поле между ннш) Поэтому, полагая в формулах (18-8) и (18-10) со = О, получае для линий постоянного тока:
Кроме того, для линий постоянного тока не приходится говорить ни о каких фазовых соотношениях, т. е. ни о каких сдвигах по фазе между токами и напряжениями. Поэтому, например, фоп. мулы (18-24) для линии постоянного тока перепишутся так:
и ==U2chax-\-l2rcShax; / =- sh ax +/3 ch ах. (18-26)
Пример 18-2. По результатам примера 18-1 определить 1) ток в Л1оскве (конец линии), 2) напряжение и ток на Волжской ГЭС имени В И Ленина в Куйбышеве (начало линии); 3) сдвиг фаз между напряжениями в начале и в конце линии; 4) к п д линии, 5) составляющие напряжения и тока в начале линии при холостом ходе (если Ux = U) и коротком замыкании (при 1 == Z), если в конце линии (в Москве) известны-
Ра = 300 МВт; С/з, = 220 кВ; cos Ф2 = 1.
Решение Положим U2 = зф = С'ф = 220 кВ
Ток в Москве при активном сопротивлении нагрузки (cos фз = 1)
h=h=-wr-=455 А.
3(72ф cos фа
Значения гиперболическихфункций от комплексного аргументау/ = 0,0906 + + / 0,962 можно найти по таблицам Но можно пользоваться формулами
shY/ = --(e -e-) = y I.0947z55-io,9!4 z-55- = 0,824 z 8623, chY/ = --(eVZ-fe~YZ) = 0,581/,7°22 ,
Напряжение и ток на ГЭС найдем по формулам (18-24): Ui = LUcb.yl + hZeihyl222 z 47 30 кВ;
h = 7- sh yl + /2 ch yl = 548 Z 63° 10 A,
T e ток в начале линии опережает по фазе напряжение на угол 1540.
Так как f/j = U., то сдвиг фаз между напряжениями в начале и в коицв линии равен 47°30
Активная мощность, отдаваемая ГЭС в линию.
Pi = 3t/i/i cos ф1 = 3 222 . 548 cos (47=30 - 63!О') = 352 МВт и к п д линии
11 = P,/Pi = 300/352 = 0,853. Составляющие напряжения Ui
(/i = f,2chY/=126,7 + ;!6,4 кВ; t/i =/а^ sh yZ = 23,3-f-/147,1 кВ. Составляющие тока.
7ix= sh у/ = -14,5 -f-/456 А, /хк = 4 ch уТСЧ + /33,9 AT
18-5. Характеристики однородной линии
В связи с тем, что напряжения и токи в линиях можно получить наложением прямых и обратных волн, принимают определенные наименования введенные выше величины. Комплексная величина у называется коэффициентом распространения, а - коэффициентом затухания, (3 - коэффициентом фазы (иногда добавляют на единицу длины). В самом деле, из формул (18-13), (18-14) и последующих видно, что а харак--терйзует затухание амплитуд прямой и обратной волн, а р, входящее в аргумент синуса, характеризует изменение фазы волны в зависимости от координаты х точки линии. Коэффициент затухания определяют в децибелах (или неперах) на единицу длины (см. пример 18-1 и § 16-1), а коэффициент фазы - в радианах на единицу длины.
Для подсчета ос и р и для построения их частотных характеристик можно обратиться к формулам
(18-27)
которые получены из (18-8). В частности, в отношении коэффициента фазы надо сделать вывод, что он монотонно возрастает с увеличением частоты.
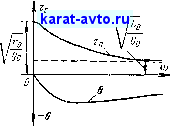
Сопротивление Zc определяет токи прямой и обратной волн по соответствующим напряжениям (18-19). Средние значения модуля Zc для воздушных линий 300-400 Ом, а для кабелей 60-80 Ом. Для кабелей емкость значительно больше, а индуктивность Lo меньше, чем для воздушных линий, так как провода у них расположены ближе друг к другу, а отно- Рис 18-4. сительная диэлектрическая проницаемость изоляции порядка 4-5. Поэтому Zc для кабелей в 6- 8 раз меньше, чем для воздушных линий.
В табл. 18-1 приведены значения первичных и вторичных параметров воздушных и кабельных силовых линий и линий связи.
Построение частотных характеристик для и S может быть выполнено по формулам (18-10) и (18-11). На рис. 18-4 даны кривые изменения модуля Zc и аргумента g волнового сопротивления для Воздушных и кабельных линий. Из выражения (18-10) видно, что при со = О
(18-28)
а при со = оо
(18-29)