
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 [ 113 ] 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248
Так как произведение корней pi и р^ характеристического урав-jjeHHH равно его свободному члену, т. е. pip = l/LC, то
= Г(( - 0. (13-40)
Напряжение на индуктивности ul найдем по формуле
UL =-Ul,.Ldi/dt = -\ [piePt-р,е^). (13-41)
Ря - Pi
Ток и напряжения на емкости и на индуктивности состоят из двух экспоненциальных составляющих, коэффициенты затухания которых равны Pi и Рз I и определены равенствами (13-35).
-е

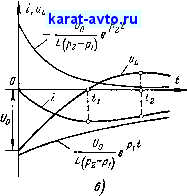
Рис. 13-18
Кривые изменения напряжений на емкости и на индуктивности тока и их составляющих приведены на рис. 13-18, а и б. Они показывают, что напряжение на емкости монотонно уменьшается с начального значения И^, а ток, возрастая от нуля, достигает максимума, а затем также уменьшается. Касательная к кривой Uc в начале координат горизонтальна, так как напряжение uq имеет максимум в начальный момент. Это следует и из второго, уже отмеченного выше начального условия i (0) == 0.
Поскольку i = С ducldt, максимум кривой тока и точка перегиба кривой напряжения uq получаются в один и тот же момент времени t. Это время можно найти, приравнивая нулю производную dildt.
Напряжение на индуктивности изменяется от значения - f/j так как при = О и ток, и напряжение на сопротивлении равны Нулю и, следовательно, напряжения на емкости и на индуктивности равны по абсолютному значению. Напряжение на индуктивности по абсолютному значению сначала уменьшается, затем проходит через нуль в момент, когда ток максимален (что следует из соотно-Н1ения Ul - L dildt), и возрастает до некоторого положительного Максимума, после чего уменьшается и стремится к нулю. Пока ток
алгебраически уменьшается (в интервале от нуля до ti), э. д. с. самоиндукции, поддерживая его, будет по закону Ленца положитель-тй, а напряжение на индуктивности отрицательным. Когда ток начинает алгебраически возрастать, э. д. с. самоиндукции противодействует ему и будет отрицательной, а напряжение на индуктивности - положительным.
Максимум кривой ul и точка перегиба кривой i получаются в один и тот же момент времени f, что следует в свою очередь из равенства Ul L dildt. Этот момент времени 4 можно найти, приравнивая нулю производную duildt.
Отметим также влияние индуктивности на протекание процесса. Из выражений (13-35) следует, что увеличение индуктивности L приводит к уменьшению абсолютных значений pi и р^, и, стало быть, к замедлению нарастания тока и спада напряжения на зажимах конденсатора. Наоборот, при малой индуктивности L ток растег быстро и быстро спадает напряжение на зажимах конденсатора. Такой случай фактически получается при разряде конденсатора через резистор (см. § 13-6).
13-11. Предельный случай апериодического разряда конденсатора
Предельный случай апериодического разряда конденсатора имеет место, если сопротивление контура г равно критическому г^р, т. е. корни характеристического уравнения (13-34) вещественные и равные:
Рг = р, = р = -г121. (13-42)
Общее решение однородного дифференциального уравнения (13-33) дается в этом случае формулой
Uc,. = Uc = {Ai-\-A4)ePK (13-43)
На основании (13-32) для свободного тока 4в получим:
JcB = i = C{A2 + pAx-\-pA2t)eP. (13-44)
-При начальных условиях uc (0) Ug и i (0) == О находим постоянные интегрирования Ai = Ug, А^ = -pUg. Подставляя значения Лх и Лз в соотношения (13-43) и (13-44), получаем ток и напряжение на емкости:
Uc = Uoil-pt)eP; (13-45)
i = CpUoteP == - еР. (13-46)
Определим также напряжение на индуктивности:
ul = LJ = -Uoil+pt)eP*. (13-47)
Кривые изменения i, uq и ul по форме не отличаются от приве-денных на рис. 13, а и б.
13-12. Периодический (колебательный) разряд конденсатора
Разряд будет периодическим или колебательным, если сопро-гйвление контура меньше критического г < г^р, т. е. корни характер истического уравнения (13-34) комплексные и сопряженные.
Обозначим в (13-35)
OL = rl2L; (13-48)
гак что
Y<y?-<=lVLC, (13-50)
\ назовем щ - угловой частотой собственных колебаний контура, а Тд - периодом его собственных колебаний. Для корней pi и р2 получим:
/01,2 = -а±/Ч- (13-51)
Решение дифференциального уравнения (13-33) при комплексных корнях его характеристического уравнения удобно записать 3 виде
Иссв = Ле- 8ш(соо^ + Х). (13-52)
Тогда ток
t, = СЛе- [- а sin (соо^-f х) + % cos (соо^ + %)]. (13-53)
Так как переходное напряжение на емкости и ток по-прежнему равны их свободным значениям и начальные условия такие же, как в двух предыдущих случаях, то по формулам (13-52) и (13-53) получим:
Uo = Aun%; 0 = СЛ (-asinx + < ocosx). Из последних соотношений находим:
Лс08Х = ~/о; tg X = ®о/а; А = [/о/соо У^С;
sinx = -7===-; cosx =
Подставляя значения Л, sin х и cos х в выражения (13-52) и (13-53) и обозначая для краткости
CmUl i = lJ й1Щ VLC = t/o/S in Х; Im = t/o/COoL,
получим окончательные выражения:
uc = и с те- sin {oot + x); (13-54)
j = / e- sin(coo-]-n); (13-55)
Ul = Uime- sin (Шо - x). (13-56)